Hacking/Cryptography
[Key Exchange] Diffie-Hellman
min_zu
2024. 12. 15. 16:48
728x90
반응형
Diffie-Hellman Key Exchange
- p : prime
- g : generator of \(Z^*_p\)
- a,b < p
DLP를 이용한다.
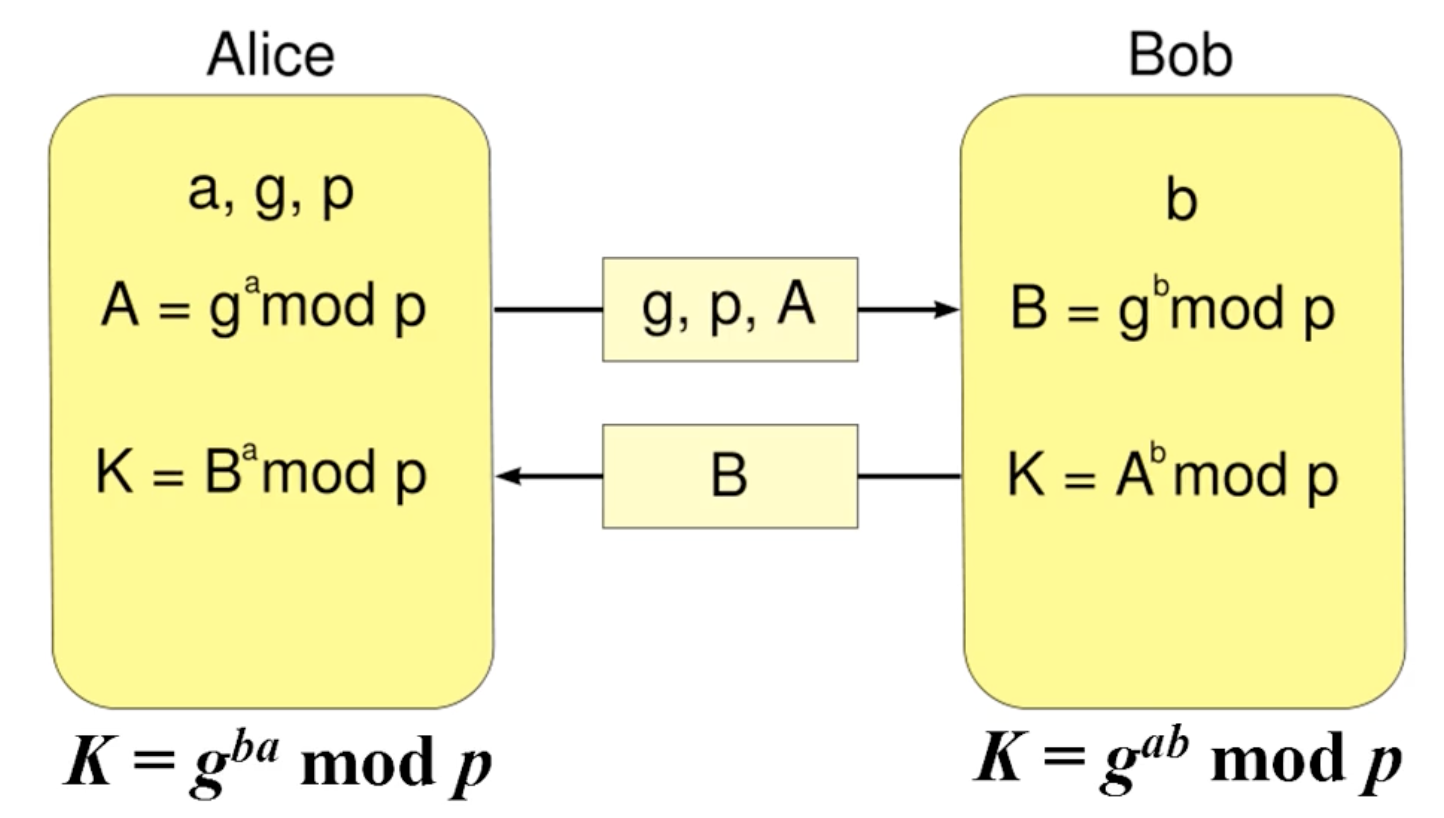
a, b는 각각 alice와 bob의 비밀키이다
해당 공개키들은 a,b 를 알 수 없다
이를 통해, 둘 만 아는 단 하나의 값을 공유할 수 있게 된다.
\(g^a\), \(g^b\)가 공개되었는데, \(g^{ab}\)를 알아낼 수 있는가?
불가능하다
하지만 비밀값을 안다면, \(g^{ab}\)를 구할 수 있다.
예시
p = 11, g = 2
Alice : a = 5, A = \(2^5\) mod 11 = 10
Bob : b = 6, B = \(2^7\) mod 11 = 7
Common key
\(g^ab\) mod p =\( 2^{5 \times 7}\) mod 11 = 10
하이브리드 암호 알고리즘
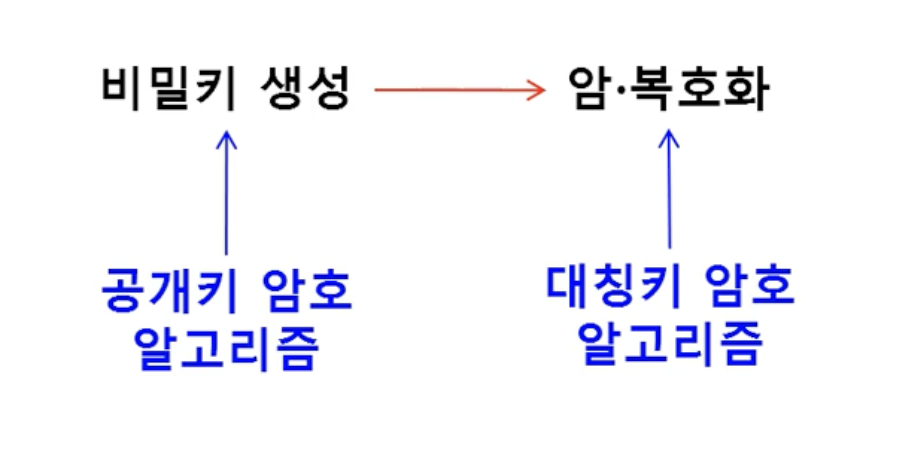
대칭키 암호 알고리즘의 장점 + 비대칭키 암호 알고리즘 장점
- 공개키 암호 알고리즘을 이용하여 비밀키 생성
-> Diffie-Hellman 키 교환 프로토콜
-> 비밀키 생성 후, 공개키로 암호화하여 전송 - 새롭게 생성된 비밀키를 이용하여 암호 및 복호 수행
728x90
반응형