Equivalence Relation
미로찾기 : 알고리즘이 달라도 성능 차이가 나지 않음

Definition of Equivalence Relation (Equivalence Relation의 정의)
Definition of Relation
- 의미가 있는 관계
- 순전히 집합으로만 정의된 관계
ex) Given a Set A a Relation on A is any subset of A \(\times\) A
A = {1, 2, 3, 4} R = {(1,3) (3,4),(1,1),(2,2)} (A\(\times\)A인 수많은 집합의 부분집합)
We write 1R3 to mean (1,3) ∈ R
extreme example) 관계가 성립한다는 것을 < 이걸로 생각할 수 있음
Relation < on N (Natural Numbers)
< = {(1,2),(1,3) ... (2,3),(2,4), ...}
2 < 4 means the same thing as (2,4) ∈ <
Equivalence Relation (동치 관계인 Relation)
같다는 관계가 조금 더 자유로운 같다
- Reflexive : For all possible a, aRa
- Symmetric : For all possible a and b, aRb implies bRa
- Transitive : For all possible a,b,c, aRb and bRc implies aRc
직관적으로 어떤 특징이 같다고 볼 수 있음
Induced Partition
Given an Equivalence Relation, a Partition is naturally induced (equivalence relation을 입력으로 받아 partition을 풀어라)
Definition of Partition : Maximal (더 이상 늘릴 수 없는) subsets \(A_i\), where if and only if a ∈ \(A_i\) and b ∈ \(A_i\), then aRb
>> 더 이상 늘릴 수 없는 부분집합 \(A_i\) <=> a ∈ \(A_i\) & b ∈ \(A_i\)이면 aRb (필요충분 관계)
* 교집합이 있을 수 없다 > 있다면 하나로 합쳐져야함
입력 : 동치관계가 성립하는 쌍을 줌 (원소 개수를 먼저 줌) (1,3) (3,9) ...
저러한 입력으로 유도할 수 있는 것들이 많음 ex) (1,3) → (3,1), (1,1)
따라서 입력은 Minimal Form 으로 주어짐 (유추가 가능한 애들은 생략하겠다)
DFS
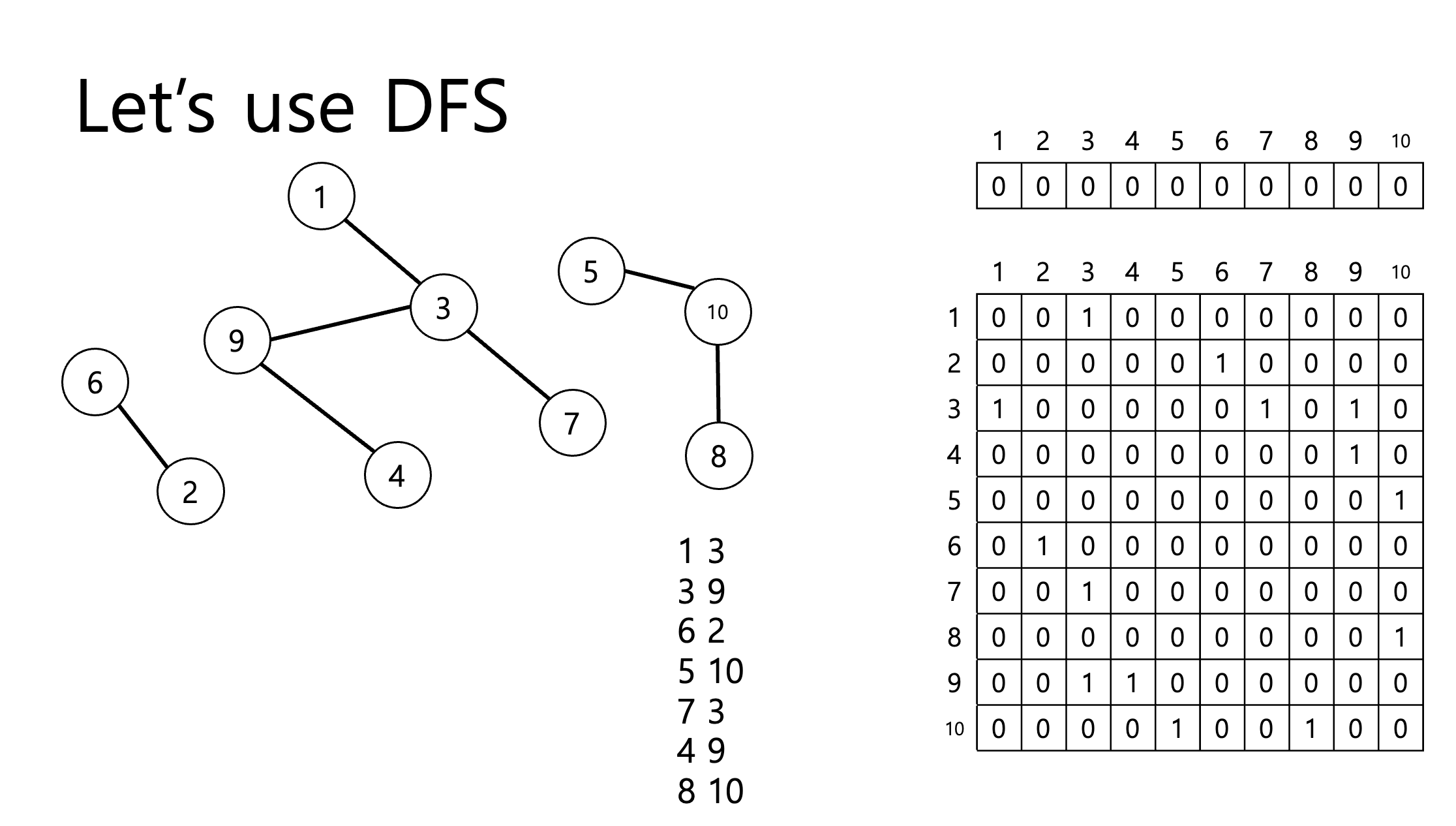
- 시작은 아무데서나 할 수 있고 목적지는 없다
- 줄이 그어져있는 곳으로 갈 수 있다 - 입력이 주어진 쌍으로만 갈 수 있음(미로찾기에서는 인접한 칸으로 갈 수 있었음)
ex) 1번 → 3번 → 9번 → 4번 → 9번 → 3번 → 7번 → 3번 → 1번 (전진하다가 갈 곳이 없으면 후진하기)
1차원 배열 : 갔는지 안 갔는지 체크하는 용도 (스택에 들어간 값들을 표시하는 느낌)
- 변수를 하나 만들어서 몇번부터 다시 봐야하는지 체크
- 별로 표시했던 1차월 배열을 출력하면 하나의 equivalence의 class 출력 가능
- 다음 dfs를 할 때는 *이 아닌 곳을 가기
2차원 배열 : 결과 - 인접하면 1을 쓰는 방법으로 표시
>> DFS에서 한번에 가는 곳들이 한 덩어리가 되는 것 > 즉 여러번 실행해야 모든 덩어리를 찾을 수 있음
구현
미로찾기와 다른 점
- 1차원 배열 만들기 - 그에 해당하는 변수도
int Map[10][10]; // 2차원 배열
char marker[10]; //어디를 들렀는지 표시할 변수
int check[10]; // 추가 변수
int start_dfs // 지난번 dfs 시작
int Stack[100];
int SP;
//DFS 한번이므로, Find 함수를 여러번 실행시켜 줘야함
int find(){
//인접한 걸 찾는데, 모든 열을 다 보아야함
while(1){
//입력받은 값을 쭉 훑기
// 들른 곳은 stack에 push
// 더 갈 곳이 없다면 pop
// 결과적으로 스택이 비면 >> 지금 표시된 곳이 한 덩어리다
}
}
* Minimal form 으로 주어져 있다는 것 : 정확성과는 상관 없음, 성능과 상관이 있음
Performance Analysis
stack, marker, Matrix 세 부분에서 쓰는 시간을 각각 생각하기
입력 사이즈는 O(n)
Matrix : n * n
On the marker
- Two options : Start from beginning every time or remember last location (매번 처음부터 보기 or 마지막 기억하기)
- Beginning : \(O(n^2)\)
- Remember : O(n)
On the stack
- 노드가 몇 번 들어갔다 나오는지 생각하면 됨 (각 node item은 한번만 들어감)
- O(n)
On the Matrix
- Two options : Start from beginning every time or remember last location (매번 처음부터 보기 or 마지막 기억하기)
- At each Column : \(O(n^2)\) and O(n)
- On the whole : \(O(n^2)\) either way
- Map의 1 개수 : 최대 O(n)개 minimal form으로 주어져있으니까 그래봣자 2배
- 한 Column에서 O(\(n^2\))을 쓰면 전체에서도 그래봤자 2배
- 어디에선가 많이 쓰게 되면, 어딘가에서는 적게 소모함
*필요한 정보만 모으면 더 빨라질 것 같다 >> 행렬을 쓰지 않고

벡터 혹은 링크드 리스트를 사용할 수도 있음
입력받은 값들을 읽어서 몇개가 있는지 확인 > malloc을 이용해서 칸을 만들어줄 수 있음
성능 : marker는 O(n) stack은 O(n) vector는 O(\(n^2\)) or O(n)(칸 수만큼 시간 - 지난번 위치를 기억하면)