int sort (int a[], int n) {
// if n <= 5 do selection sort
// else
int p = a[0]
int i = 1; int j = n-1;
while (i < j){
while (a[i] < p && i < n) i++;
while (a[j] > p) j--;
if(i < j) swap a[i], a[j];
}
swap a[0] and a[j];
//Divide and Conquer
sort(a,j);
sort(a+j+1, n-j-1);
return;
}배열을 추가로 할당하지 않는다.
0, 1, 2 ... j, j+1 ... n-1까지의 인덱스를 가진 배열로 가지고 있다.
0(a)부터, j-1까지 재귀호출을 한다.
j를 제외하고
a+j+1부터, n-1까지 재귀호출을 한다 .
재귀호출을 끝내면 바로 끝난다. *Merge는 재귀 호출 후 다시 merge 해야함
재귀호출을 하고 끝나게끔 미리 setting을 해둔것이다.
a[j]가 꼭 중간이 아닐 수도 있다.
a[j] 전에 있는 것들은 모두 a[j]보다 작고, 후에 있는 것들은 모두 a[j]보다 크다.
그렇게 재귀를 돌리기 전까지 setup을 한 것이다. (while 문에서)
<sorting 전 과정 설명>
p = a[0] pirot (아무거나 잡아도 되지만 왼쪽이 편함)
이 p가 결국 a[j]가 될 얘이다.
i = 1(배열의 두번째 원소) j = n-1 (배열의 오른쪽 끝)

현재 이런 상태가 된다.
a[i]가 p보다 작다면, i를 증가시킨다.
a[i]가 p보다 크다면, j를 감소시킨다.
p보다 작은 것을 다 건너뛰고, 중간에 멈추게 되고, j 가 큰것을 다 건너뛰고 중간에 멈추게 된다.
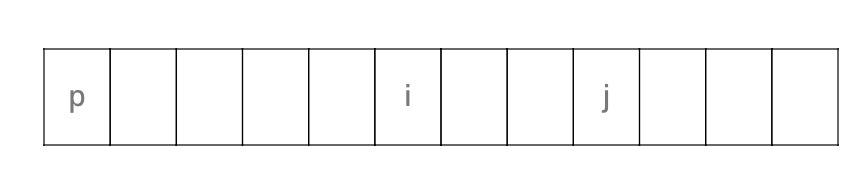
즉, 현재 i에 있는 것은 p보다 크고, j에 있는 것은 p보다 작다.
따라서 작은 것을 전부 왼쪽에 , 큰것을 전부 오른쪽에 넣고 싶기 때문에 i와 j에 있는 값을 서로 바꿔준다.
이를 반복하여 다 작은건 왼쪽, 큰건 오른쪽으로 오게 만들고 p와 j의 위치를 바꾼다.
이렇게 이상한 과정을 거치는 이유는 하나의 배열을 또 만들지 않기 위해서이다.
배열을 추가로 할당한다면 merge sort보다 느려짐
qucik sort를 더 많이 사용한다.
Performance
왼쪽이 k개라면, n-k-1개가 된다.
성능이 좋은 것은k가 n/2가 되면 O(nlogn)의 성능을 보일 수 있다.
하지만, 만약 피벗이 맨 오른쪽에 있다면, n-k-1개가 0이 되고, 계속 k-1개, k-2개.. 으로 재귀호출을 하게 되고 O(\(n^2\)) 의 시간이 걸림
그럼 피벗을 어떻게 하여 잘 잡을것인가?가 문제가 된다.
- Worst case : T(n) = T(n-1) + n = T(n-2) + n + n ... = O(\(n^2\))
- Best case : T(n) + 2T(n/2) + n = ... = O(nlogn)
- Average case : All possible cases with same probability
Average case
평균적인 case
모든 가능한 경우가 n!가지가 있는데, 그냥 더할 수 있다.
E(x + y) = E(x) + E(y)
n!가지를 다 따로 더해서 할 수 없기 때문에
피벗이 가장 작은 경우, 두번째로 작은 경우 ... 가장 큰 경우 이런식으로 나눌 것임
즉, 피벗이 (n-1)! 경우가 있다.
모든 경우에 대한 기댓값을
T(n) = \(\frac{1}{n}\)(T(n-1)) + \(\frac{1}{n}\)(T(1) + T(n-2)) + .... = \(n + \frac{1}{n} \sum_{k=0}^{n-1}\{T(k) + T(n-k+1)\}
T(n-1) = \(n-1 + \frac{1}{n-1} \sum_{k=0}^{n-2}\{T(k) + T(n-k-1)\}\)
이를 계산하면,
nT(n) = \(n^2 + 2(T(1) +... T(n-1))\)
(n-1)T(n-1) = \((n-1)^2 + 2(T(1) + ... T(n-2))\)
이 두개를 빼주면
nT(n) - (n-1)T(n-1) = 2n -1 + 2T(n-1)
nT(n) = 2(n-1) + (n+1) T(n-1)
\(\frac{T(n)}{n+1} = \frac{2n-1}{n(n+1)} + \frac{T(n-1)}{n}\)
을 \(a_n\)이라 하면
\(a_n\) = \(a_{n+1}\) + \(\frac{3}{n+1}\) - \(\frac{1}{n}\)
n= 1일때부터 n=n일때까지 더하면
\(a_n\) = 2(1 + 1/2 + 1/3 + 1/4 ... 1/n)과 같다.
따라서 y = 1/x의 넓이와 비슷하고, 이는 log n 이다.
\(\frac{T(n)}{n+1}\) = log n 이므로 T(n) = nlogn과 비슷하다.
∴ O(n log n)