전자 서명
- 전자 문서에 대한 데이터 인증 및 사용자 인증

- 서명 생성자만 서명을 할 수 있어야함
- 다른 누군가에 의해 위조될 수 없음
- 서명을 생성한 것을 거부할 수 없음
- 누구나 서명 생성자를 확인할 수 있어야함
서명 -> 서명 생성자의 신원 확인, 서명의 유효성 검증, 위조 불가능성, 부인방지
공개키- 개임키 쌍이 인감 도장이 되고, 두 사람의 공개키는 공인 인증기관에 등록되고 검증되어 사용
* 암호화와 서명은 목적이 다르다. 데이터의 기밀성(내용 숨김)과는 전혀 관련이 없다
S = sig(M, 개인키) : 서명은 서명 생성자만 할 수 있음
M = Verify (S, 공개키) : 서명 생성자의 공개키(누구나 아는 것)으로 서명을 확인할 수 있음
즉, 개인키와 공개키를 이용하여 서명의 기본 기능을 제공해준다
-> 인감이 되어야함 = 공개키가 누구의 것인지 알아야한다.
공개키는 랜덤 값에 불과한데, 이를 공개키를 관리하는 인증 기관에 등록하여 인증서를 발급받으면 이를 통해 서명을 검증할 수 있다.
목적
- 전자 문서의 위변조 방지
- 문서의 내용과 서명자에 대한 인증 -> 문서 내용의 무결성 / 서명자의 신원 인증
- 전자 서명의 보안 요구사항
- 위조 불가 (Unforgetable) : 서명자만이 전자 서명 생성
- 인증 (Authentication) : 전자 서명의 서명자를 확인 가능
- 재사용 불가 (Not Reusable) : 한번 생성된 서명을 다른 문서의 서명으로 사용 불가
- 변경 불가 (Unalterable) : 서명된 문서의 내용 변경 불가 / 데이터의 무결성 보장
- 부인방지 (Non Repudiation) : 서명자가 나중에 서명한 사실을 부인할 수 없음
기능
비대칭키를 이용한 부인방지 확보
- 철수는 영희에게 편지를 보낼 때 자신의 사설키로 편지를 암호화
- 철수의 공개키로만 복호화 가능
- 영희는 그 편지가 철수가 쓴 것임을 확신

서명할 때는 서명자의 개인키를 사용하고 서명을 확인할 때는 공개키를 사용한다. (암호화와 다른 부분)
즉, 암호화와 서명의 키 사용 방식이 거의 반대된다. -> 기능이 반대이기 때문
전자 서명의 생성
암호문 : M -> C -> M
서명 : M + S
즉, 서명은 서명 생성 알고리즘에 의해 원래 문서에 추가정보가 추가되어 데이터 사이즈가 매우 커진다.
원래 문서 자체에 대해서 서명 알고리즘을 돌리게 되면, 원래 문서 크기 만큼의 서명이 생성이 됨.
따라서, 서명을 추가하면 원래 문서의 크기가 2배가 된다.
전자 서명의 두 가지 핵심 중 하나이다.
- 개인키, 공개키를 사용한다
- 주어진 메세지를 암호학적 해시 함수를 통해 서명을 덧붙임
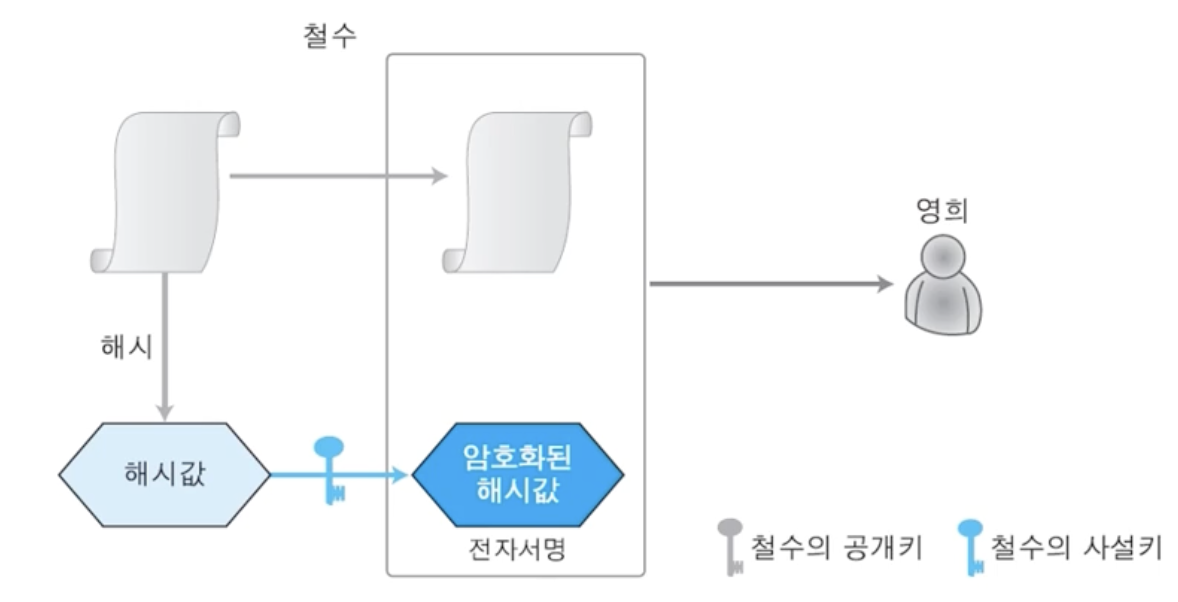
해시는 총 3가지 기능을 제공한다.
- 메세지 크기 축소
- 메세지 무결성 제공
- 재사용 방지
해시 값을 생성자의 비밀 키로 암호화한다.
해시 : SHA-1, MD5
해시 값으로 서명하게 되면, 고정된 길이의 값으로 나오게 된다.(160~256)
따라서 서명의 길이도 줄어들게 된다.
S = sig(H(M), 개인키)
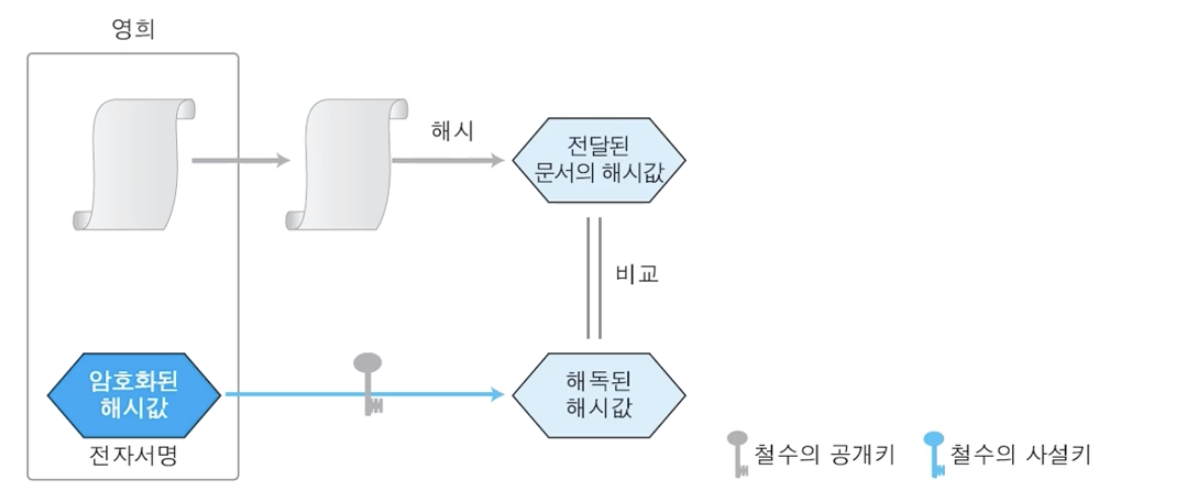
전자서명 검증
- 주어진 문서(원본 문서)의 해시 값
- 서명 생성자의 공개키로 서명 복호화 -> verify(s, 공개키)
- 두 가지가 같은지 비교
전자서명 알고리즘
- RSA Signature -> 소인수 문제에 기반
- DSA (Digital Signature Algorithm) -> DLP 문제에 기반
- KCDSA (Korean Certificate-based Digital Signature Algorithm) : 국내용
RSA Signature
Public key
- n = pq
- e mod (p-1)(q-1)
Private key
- p, q
- \(d \equiv 3^{-1}\) mod (p-1)(q-1)
Signature
- S = \(M^d\) mod n
- 개인키로 서명을 생성함
Verification
- M = \(S^e\) mod n
- = \(M^{de}\) mod n = M mod n (RSA 증명과 같음)
결국 원본 문서와 서명된 문서를 둘 다 해시한 결과를 비교하면 됨
위처럼 그대로 사용할 때는 문제가 하나 생긴다.
공격자가
\(S_1 = M_1^d\) mod n
\(S_2 = M_2^d\) mod n
두 가지 서명을 알고 있다고 하면
\((M_1 \cdot M_2)\)에 대한 새로운 서명 S'를 생성 가능하다
\(S_1 \cdot S_2 = M_1^d \cdot M_2^d\) mod n = \((M_1 \cdot M_2)^d\) mod n 으로 생성 가능하다.
물론, M1, M2를 곱한 메세지에 의미는 없지만, 본인이 아닌 다른 사람이 서명을 생성할 수 있는 것만으로도 문제가 된다.
Q) 이걸 어떻게 해결이 가능한가?
A) 해시의 역할이다 -> 재사용 방지
해시를 시킨 결과로 확인하면
\(S_1 = H(M_1)^d\) mod n
\(S_2 = H(M_2)^d\) mod n
\(S = (H(M_1) \cdot H(M_2))^d\) mod n이다.
실제 \(M_1 \cdot M_2\) 는 \(H(M_1 \cdot M_2) ^2\) mod n이 된다.
DSA(Digital Signature Algorithm)
- For two primes p, q (q < p)
Public Key
- \(y = g^x\) mod p
Private Key
- choose x at random, 0 < x < q
Signing (M)
- for a random k, 0 < k < q
- r = (\(g^k\) mod p) mod q (단 r != 0)
- s = (\(k^{-1}\)H(M) + xr)) mod q
- Signature <M,r,s>
Verifying
- w = \(s^{-1}\) mod q
- u1 = H(M)w mod q = H(M) / s-> 원본 메세지에 대한 해시 생성
- u2 = rw mod q = r / s
- v = (\((g^{u1}y^{u2})\)mod p) mod q = \(g^{\frac{H(M)}{s}} \cdot g^{x\frac{r}{s}} = g^{\frac{H(M+xr)}{s}}
= g^{\frac{H(M) + xr}{k^{-1}(H(M)+xr)} = g^k\) - check if v = r
해시
- 하나의 문자열을 이를 상징하는 더 짧은 길이의 문자열로 변환 : 입력문의 길이와 상관 없이 동일한 길이의 문자열 ㅜㅊㄹ력
- 암호학적 해시 함수
- Collision-Resistant (충돌 방지) : 한 비트만 달라도 결과가 완전 다름
- One-Wayness (일방향성) : 해시값으로부터 원문을 추측하기는 불가능
암호와는 다르게 복호화가 불가능함. 즉, 해시는 암호화하는 방법이 아니다.
MD5
- RSA와 함께 공개키 기반 구조를 만들기 위해 개발
- 32비트 컴퓨터에 최적화
- 32개의 16진수로 출력 (128비트)
SHA(Secure hash Algorithm)
- NSA에 의해 고안
- 0 < |M| < \(2^64\)
- 512비트의 입력 블럭 (16 * 32bits)단위로 hashing -> CBC 처럼 해시 값을 만듦
- 160비트의 해시 결과 생성
Message padding
- 입력문의 총 길이가 n * 512 : 원 메세지 + 1 + 0 + 0 ... 0 + 원 메세지의 길이(64bit)
- \(M_1\), \(M_2\), ... \(M_n\)개의 블럭 : 각 블럭을 순차적으로 hashing
하나의 블럭 \(M_i\)
- 16개의 word(32bits)로 구성
- SHA-1에서 정의된 함수(f)와 keyword(상수)를 이용
- 80회의 연산 수행
- 각 32비트짜리 5개의 블럭 (A,B,C,D,E)생성%
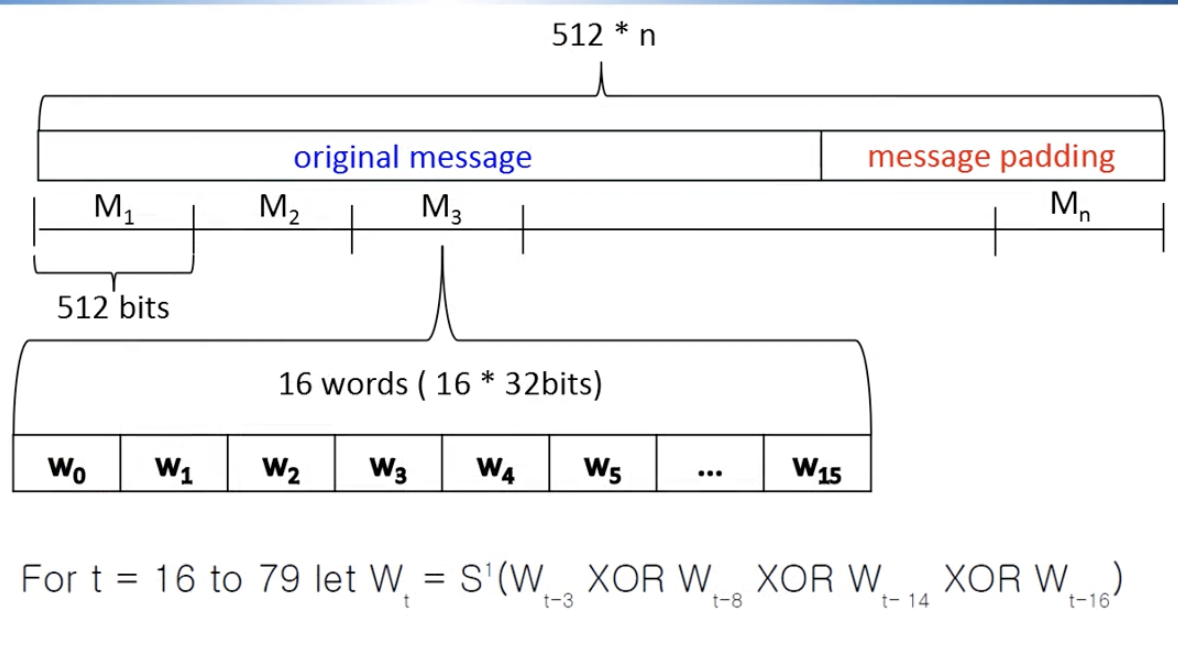
16개의 워드는 512에서 잘라서 만든다.
16~79 워드는 이전의 워드로 만든다. -> 해당 식을 기반으로 만듦 (shift 1)
80개의 워드로 어떻게 160bit를 만드는지
지금 위의 입력은 초기값이 지정되어 있는 해시이다 즉, 160bit -> 160bit 이다
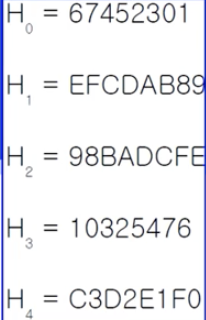

A가 다양한 블록으로 된다.


몇번째 블록인지에 따라 사용하는 회전 함수와 K가 다르다
이렇게 ABCDE의 값을 섞는 과정이 80번이고 이를 반복하며 첫번째 블록에 대한 해시가 만들어진다.
두번째 메세지 블록에 대해서는 어떻게 적용되는가?
그 이전 블록의 ABCDE 값에 대해서 H0 = H0 + A.. 으로 계산하여 H0~H4를 정해 해시 연산을 한다.
∴ 해시는 정보의 무결성을 확인하는 것
'Hacking > Cryptography' 카테고리의 다른 글
| [전자상거래] SET 프로토콜 (0) | 2024.12.15 |
|---|---|
| 공개키 기반 구조(PKI) (1) | 2024.12.15 |
| [Key Exchange] Diffie-Hellman (0) | 2024.12.15 |
| [비대칭키 암호 시스템] RSA (0) | 2024.12.15 |
| [비대칭키 암호 시스템] Elgamal Encryption (1) | 2024.12.15 |