Stack
- Push(Insert) / Pop(Delete)만 제공함
- Last in, First out
Q. Stack을 가지고 sorting 할 수 있는가?
A. 안되는 경우 : 3, 8, 2와 같이 중간수, 큰 수, 작은 수의 순서가 전체에 한번이라도 등장하면 sorting 할 수 없음
Q. 함수 호출 시 스택
A. a함수가 b함수를 , b함수가 c함수를 실행시킨다면, c, b, a 순으로 리턴됨 스택의 구조와 같다.
성능
- Push : O(1)
- Pop : O(1)
구현

Stack Pointer : 빈 자리를 가리키는 ( 개인 취향 ) 배열 인덱스 (보통 빈 자리를 가리킴) - 배열의 크기(가용)을 나타내기도 함
//Stack 구현
int Stack[100]; //Stack
int SP; //stack pointer
int init() {
SP = 0;
return 0;
}
int isEmpty() { //비어있는지 확인
return SP == 0;
}
int Push(int x) {
Stack[SP++] = x; //넣은 후 증가
return 0;
}
int Pop() {
return Stack[--SP]; //감소 후 제거
}
//생략된 함수들
//isFull() 꽉 찼는지 확인하는 함수 - 스택은 꽉 차면 사용 불가
//top을 확인하는 함수
Queue
- Insert / Delete만 제공함
- First in, First out
성능
- Insert : O(1)
- Delete : O(1)
구현
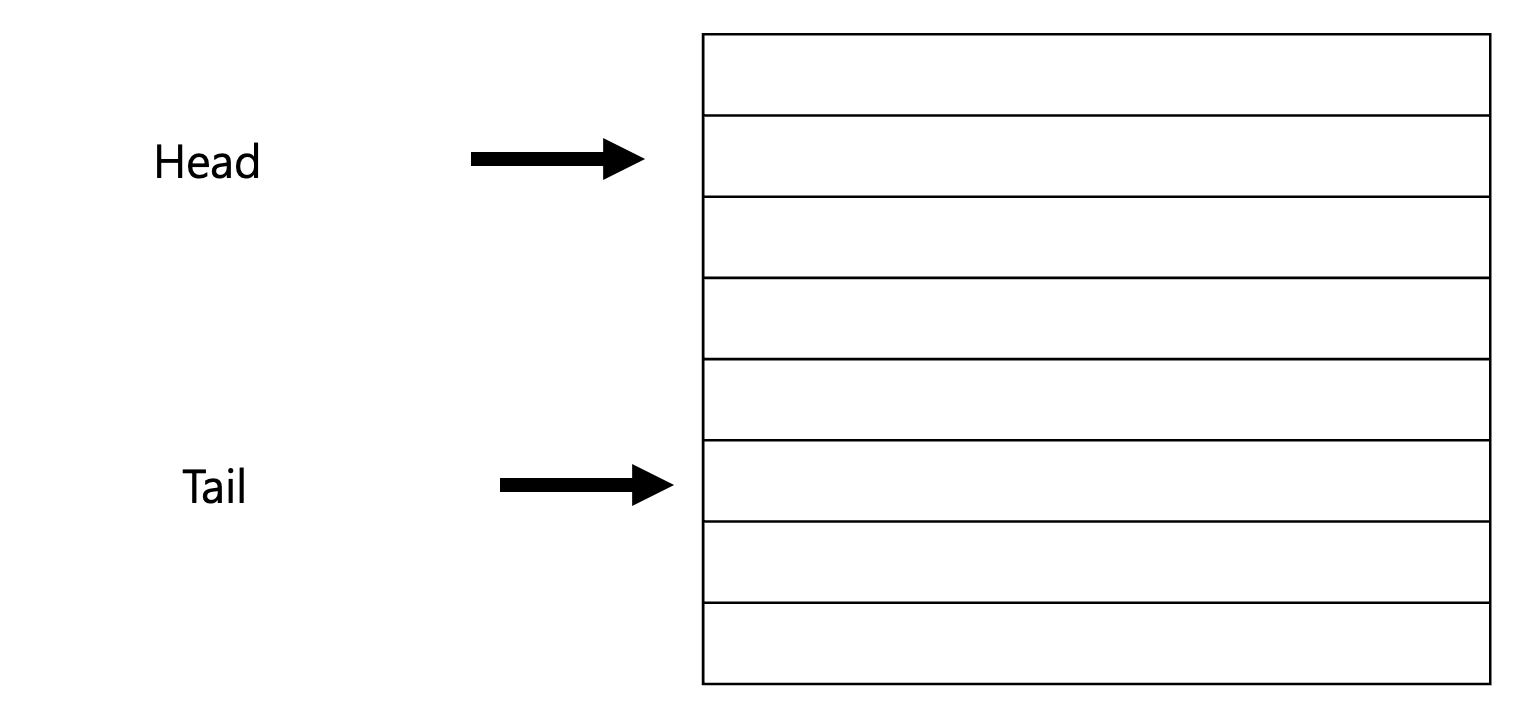
Head : 시작 위치 ( 자료를 꺼낼 위치를 가리킴)
Tail : 끝 위치 (자료를 삽입할 위치를 가리킴)
Head 와 Tail 이 같다면 ? : 비어있음? - 하지만 꽉 차면 head와 tail이 같아질 수 있음
>> 해결하기 위해 변수를 만들어서 꽉 찬 여부를 확인해줌
>> 최근에는 한 칸을 그저 비워놓고 사용하는 방법을 사용함
int Queue[N];
int Head, Tail;
int init(){ Head = Tail = 0;}
int isEmpty() { return Head == Tail; }
int insert(int x){
Queue[Head] = x; Head = (Head + 1) % N; //허용 범위를 넘어도 사용하기 위함
return 0;
}
int delete(){
int RetVal;
Retval = Queue[Tail]; Tail = (Tail + 1) % N;
return RetVal;
}응용 (DFS / BFS) - 미로찾기
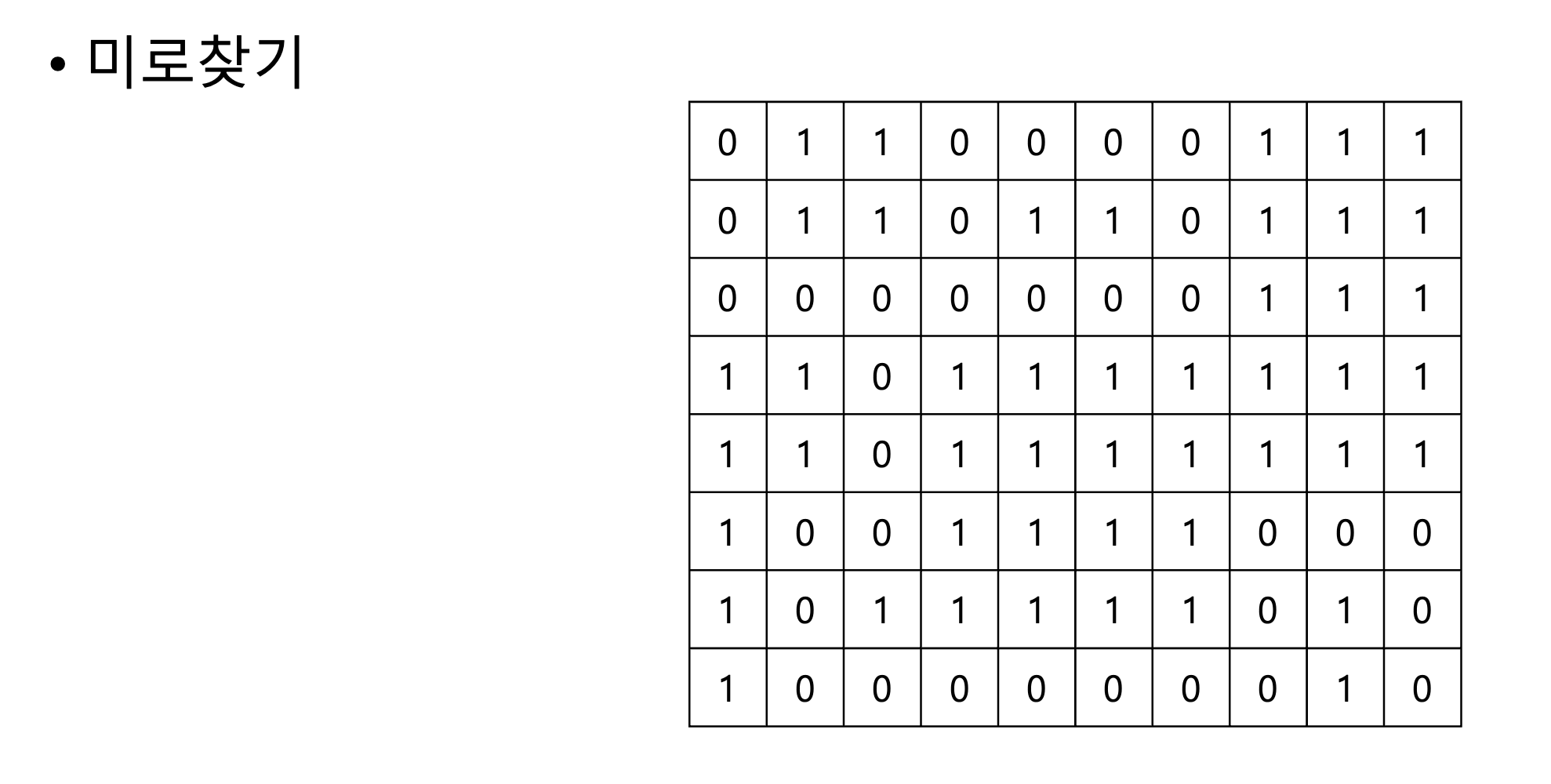
- 왼쪽 상단의 (0,0)에서 시작
- 0은 진행 가능한 길, 1은 벽
- 매 칸을 방문할 때마다 방문함을 표시해야함
DFS 명시적 Stack
* 명시적 stack? : call stack을 쓸 수 있음 (재귀호출 할 수 있음)
- 끝까지 가보고 다시 분기점으로 돌아와서 다른 방향으로 감 (실을 풀었다가 다시 감는것 처럼)
- 스택과 같이 가장 나중에 갔던 길에서부터 다시 돌아옴 (실을 끝에서부터 감으니까)
- 전진하는 것을 재귀호출로 짤 수도 있음
int Find(){
i = j = 0;
if(Map[i][j] != '0') {
printf("시작 지점(0,0)에서 출발할 수 없습니다.");
return 0;
}
else{
Map[i][j] = '*';
while(1){
if(i == M-1 && j == N-1) {
Map[i][j] = 'X';
return 1;
}
if(Map[i-1][j] == '0') {
if(i == 0) continue;
Push(i); Push(j);
i = i-1; j = j; //상
Map[i][j] = '*';
}
else if(Map[i+1][j] == '0') {
if(i == M-1) continue;
Push(i); Push(j);
i = i+1; j = j; //하
Map[i][j] = '*';
}
else if(Map[i][j-1] == '0') {
if(j == 0) continue;
Push(i); Push(j);
i = i; j = j-1; //좌
Map[i][j] = '*';
}
else if(Map[i][j+1] == '0') {
if (j == N-1) continue;
Push(i); Push(j);
i = i; j = j+1; //우
Map[i][j] = '*';
}
else{ //상하좌우에 갈 길이 없는 경우 후진
if(isEmpty()) return -1; //시작 위치에서 감으려고 하면 실패
Map[i][j] = '*';
j = Pop();
i = Pop();
}
}
}
}DFS 명시적 Stack의 정확성
증명할 것 : 시작위치에서 갈 수 있는 곳은 전부 다 간다. (길이 있으면 간다)
< 갈 수 있는 곳이라는 의미 >
- (0,0)에서 어떤 위치 (s,t)로 가는 길이 있다.
- (0, 0), (a1, b1), (a2, b2), …, (s, t)인 좌표 sequence가 있고 인접한 쌍에서는 두 좌표가 각각 최대 1차이이다.
- Map의 모든 좌표에 초기에 0이 적혀 있다
< 증명 >
귀류법을 사용하자.
갈 수 있는 곳인데 못 갔다고 가정하기
Q. 방문한 곳과 방문하지 못한 곳이 붙어있을 수 있는가?
A. 코드를 살펴보면 가능한 모든 곳을 방문하기 때문에, 방문한 곳과 방문하지 못한 곳이 붙어있을 수는 없다. 만약 방문했다면 그 옆에가 방문할 수 있는 곳이라면 무조건 방문하게 되어있다.
∴ 방문한 곳과 방문하지 않은 곳이 붙어있을 수 없기 때문에 모순 (아직 전진을 하지 않은 경우가 있을 수 없다)
* 한 칸에서 일어나는 일들만 모아서 생각하면 좀 더 간단하게 생각할 수 있음 (시간 순으로 생각하지 말자)
[ 한 칸에 다시 방문하는 경우 생각해보기 ]
만약 8방향이라면, 최대 7번 방문 가능 전진 후 후진해서 다른 방향으로 전진하는 경우가 7번 있을 수 있음
그 이상 다시 방문할 수 없음
ex) 갈 수 있는 방향은 3개 > 전진은 3번 이하 할 수 있음
왜? 뒤로 돌아가서 다시 전진할 수 있는데, 이미 온 길은 더 이상 0이 아니기 때문이다.
출발할 때 0이였다고 해서 다시 돌아왔을 때도 0이라는 보장이 없기 때문이다
DFS 명시적 Stack 성능
한 칸에서 일어나는 일들을 생각해보자
- O(mn)
한 칸에 도착했을 때 하는 일 - 상수시간
전체시간 - 칸 개수
BFS 명시적 Queue
- 주변에 0인 칸이 있으면 무조건 집어넣기
- 다음에 가는 곳은 인접한 칸이 아닌, Queue에서 꺼내서 가는 것 (i,j가 무조건 pop 한 것이 됨)
- 같은 칸이 Queue에서 여러번 나올 수 있음
- 여러번 나오면 무시하도록 코드를 짜야함
int Map[M][N];
int i, j;
inf Find(){
i = 0; j = 0;
while (1) {
if (Map[i][j] == '*') {if(IsEmpty()) ...}
Map[i][j] == '*'
if(Map[i-1][j] == '0') {Insert(i-1); Insert(j)} // *8
if (IsEmpty()) break;
i = Pop(); j = Pop();
}
}
STEP
4 방향이라고 가정하면
queue가 갈 수 있는 방향이 a,b라고 가정하면
queue에 a,b가 들어가고 a를 꺼내서 a로 감 (b는 그대로 들어있는 상태)
a에서 갈 수 있는 방향은 c,d
queue에서 다음에 뽑으면 b
방금 간 곳의 근처를 간 곳을 가는게 아닌, 가까운 곳 부터 가게 됨
즉, 거리가 3,4인 애가 있다면, 거리가 3인 곳을 먼저 가야만 거리가 4인 곳을 갈 수가 있음
'CS > Data Structure' 카테고리의 다른 글
| Linked List (2) | 2024.04.21 |
|---|---|
| Equivalence Relation (0) | 2024.04.21 |
| String Matching (0) | 2024.04.12 |
| [ Arrays for search, insert, delete ] Unpacked unsorted & Unpacked sorted (1) | 2024.04.10 |
| [ Arrays for search, insert, delete ] Packed sorted (1) | 2024.04.10 |