Closest pair
- Computational Geometry
- 직관과 심하게 충돌하는 경우 많음
- 주어진 점들 중에서 가장 가까우 쌍을 찾기(2차원)
Usually Input is given by Coordinates
좌표 형태로 입력이 들어온다.
(a,b), (c,d)가 주어진다면 -> \(\sqrt{(a-c)^2 + (b-d)^2}\) 을 모든 쌍에 대해서 하면 \(n^2\)개가 생기고 이 중에 제일 작은거 찾으면 됨
sqrt()라는 함수로 루트를 계산할 수 있지만, 무리수이기 때문에 정확한 계산이 불가능하다.
1 - Dimensional Version

sorting 후, 가장 옆에것과의 거리를 비교하여 가장 짧은 것을 고르면 됨
Divide and Conquer

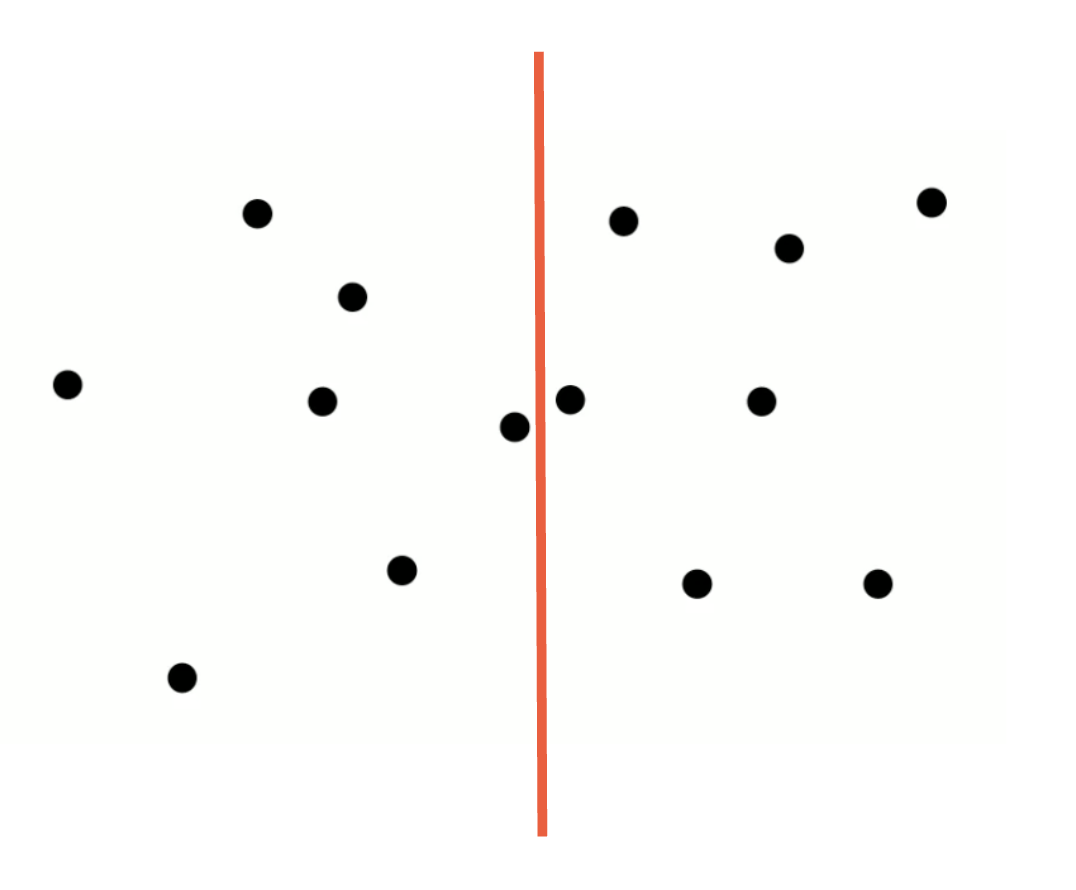
First, Sort by x coordinates and divide, recurse
x좌표를 기준으로 sorting 한 후, 절반을 나눈다.
가상의 선을 긋는 것이다. 배열을 절반으로 나누고 Left와 Right라고 생각하는 것 뿐이다.
1 일때는 거리가 없기 때문에, 2를 base로 하여 재귀적으로 풀 수 있을 것이다.
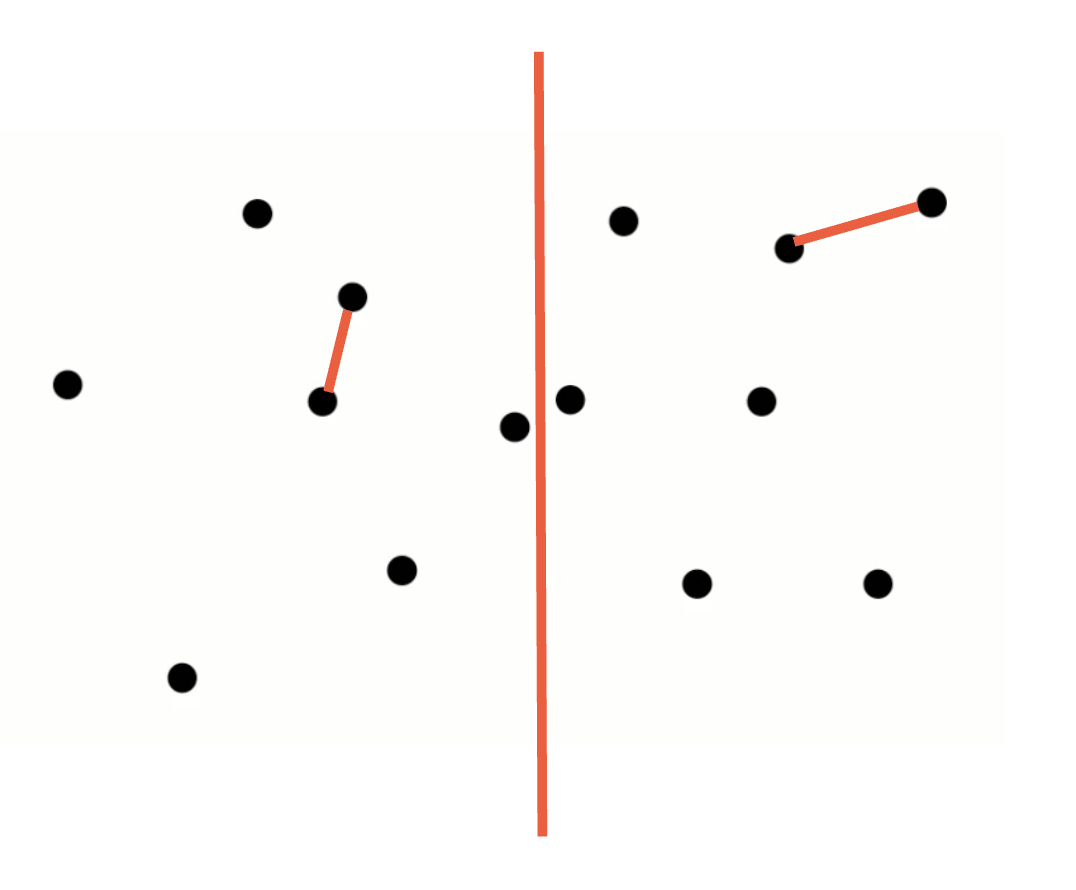
We have DL and DR.
Let D = min(DL, DR)
왼쪽에서 가장 가까운 쌍을 구하고, 오른쪽에서 가장 가까운 쌍을 구했다고 생각하자
가능한 전략
1) 왼쪽 점 - 오른쪽 점 모든 쌍 -> \(n^2\)
2) band만듦 왼쪽으로 d만큼,오른쪽으로 d 만큼 가서 그 영역을 band라고 하고, 그 안에서만 비교 -> 점들이 상당히 줄어들 수 있음
* 만약 점들이 엄청나게 분산되어 있거나 엄청 몰려있다면 의미가 없다. -> 최악의 경우 \(n^2\)
Key Observation (Difficulty #1)
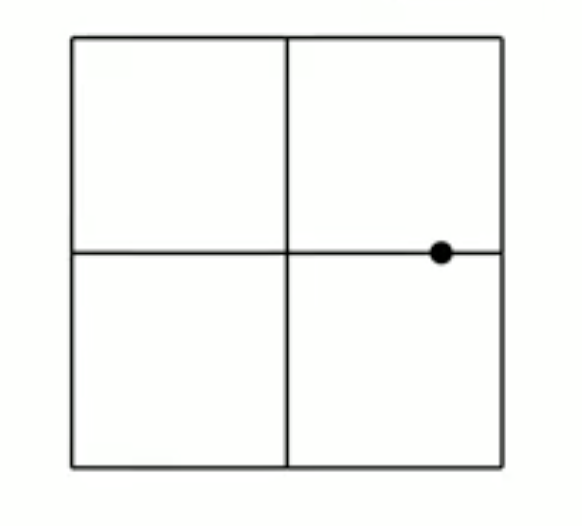
- Comparing points within the Band may take \(O(N^2)\) time
- How Many Points within one Square? (with side len D)
band의 일부만 본 그림이다.
변 길이가 d인 정사각형 4개를 그린 것이다.
band 안에 있는 점들만 비교하면 된다. -> 밴드 밖에것은 비교할 필요가 없음
*이미 왼쪽에서 작은 것, 오른쪽에서 작은 것을 찾았다고 생각하자
따라서 중앙선을 기준으로 저 점은 오른쪽 점들과 비교할 필요가 없다.
Q) 정사각형 안에 점이 얼마나 있을까? 수없이 많을 수 있을까?
A) 그럴 수 없다.
왜냐하면 굉장히 많은 점들이 있다면, 가장 가까운 것이 정사각형 안에 생긴다. 현재 D는 가장 짧은 거리이다. D= min(DL, DR)
따라서 D보다 가까운게 없다는 가정 하에 한 정사각형 안에 최대 3개를 넣을 수 있다. 그 이상을 넣는다면 길이가 D이하인 점이 나온다.
왼쪽에 엄밀히 따지면 최대 5개 넣을 수 있음
남은 문제 : 저 금은 점 입장에서 왼쪽에 5개 점을 찾아야한다.
Strategy
- Sort points within the Band by y coordinates
- Fromm Lower to Higher
- Compare each Point to the next 5 points
x좌표를 sorting 한 상태의 배열이다.
D = min(DL, DR)인데, D=50이라고 가정하고, 현재 배열에서 중간을 보면 (70,50)(80,75) 사이로 오른쪽 왼쪽이 나누어져있다고 하자
25부터 125까지가 band 영역이 된다.
따라서 band에 있는 좌표를 잡는 것은 쉽다.
이제 band에 있는 점들만 따로 배열에 넣는다 -> 이제 band에 있는 점들만 가지고 있음
y를 기준으로 sorting한다.
모든 점들은 자신보다 "위"에 있는 점들의 거리만 계산한다. (양방향의 계산이 필요하지 않도록)
band에 있는 얘들 중에 다섯개를 본다. (왼쪽, 오른쪽에 있던 상관 없이) -> y좌표로 sorting해서 위에 있는 것만 볼 것이기 때문이다.
이때 D보다 작은 것이 있다면, 그것이 정답이 된다.
=> O(N x logN x logN) time -> O(nlog\(^2\)n)
How to make it O(NlogN)?
- Sort All points by y coordinate (Difficulty #2)
- Comparison still works in O(N) (HOW?)
- Sort by y becomes Merge by y (WHY?)
밴드에 있는 것만 sorting 하지 말자
y좌표로 sorting을 모든 점을 sorting하자.
원래는 밴드만 뽑아서 sorting 한 후, 5개를 봤는데,
지금은 밴드에 있지 않은 것도 sorting하니까, 더 멀리 가서 5개를 비교해야한다.
for(i = 0; i < x; i++) fori(j = i+1; j <= i+5; j++)
그렇게 하더라도 시간이 늘어나지 않는다.
band에 있지 않은 "쓸데없는것"을 지나서 5개를 찾느넫, 쓸데 없는 것도 5번 지나간다.
band만 있는 경우에도 그 점을 5번 지나간다.
결국 band에 있지 않은 것을 비교하더라도 비교하는 시간이 늘어나지 않는다. x는 그냥 지나치기 때문이다. -> O(N)
필요 없는 계산을 했더니 시간이 줄어들었다
sort by x를 한 후에는 또 sort할 필요가 없음. 맨 위 레벨이 아닌 아래 레벨에서는 sorting이 필요하지 않음.
재귀가 끝나고 올라왔을 때, 모든 좌표를 y로 sorting한다고 하자.
아래쪽에서 끝날 때 y좌표로 sorting된 상태로 return했다고 하자.
따라서 L과 R이 이미 sorting되어있고, 맨 위에서는 merge만 하면 된다. -> O(N)
=> O(nlogn)
Plane Sweeping
처음에 점들을 x좌표로 sorting 해놓고 시작한다.
수직선을 오른쪽으로 옮겨가면서 문제를 푸는 것
각 점을 기준으로 수직선을 긋는다.
수직선 자체가 어떠한 자료 구조(TREE) 를 가지고 있다.
d = 지금까지 본 가장 가까운 거리
tree = band의 점들이 y로 sort되어 저장 (AVL 등)
다음 좌표로 수직선이 점프하면 없어지는 점들이 존재하고, 그러한 점들은 x좌표로 sorting된 배열에서 왼쪽부터 빠지면 된다.
새로 들어온 점의 y좌표를 기준으로 정사각형을 그린다.
이를 Tree에서 찾고 더 작은게 있다면 d를 수정한다.
=> O(NlogN)
'CS > Algorithm' 카테고리의 다른 글
| [ Divide and Conquer ] Farthest Point (3) | 2024.12.04 |
|---|---|
| [ Divide and Conquer ] Convex Hull (1) | 2024.10.23 |
| [ Divide and Conquer ] The Selection Problem & Approximate Median (2) | 2024.10.20 |
| [ Divide and Conquer ] Recursive Merge Sort (0) | 2024.10.20 |
| [Greedy Algorithm] Tape Storage (0) | 2024.10.20 |