Smallest Convex Polygon containing all the points
모든 점을 포함하는 가장 작은 볼록 다각형
작다라는 것은 면적도 가장 작고, 변의 길이와 변의 개수가 모두 작은 것을 의미한다.
-> 직관적으로 이해하려면, 밖에 고무줄을 두른다고 생각했을 때 딱 들어가는 것을 convex hull 이라고 할수 있다.


결국은 이 문제가 NlogN에 풀린다.
Q) NlogN보다 빠를 수가 없다.
A) 점들이 원 모양으로 좌표에 있다고 하면, 이걸 이은것이 convex hull이다. 그러니, 무작위 좌표값을 각도로 sorting을 하고 이어야한다. 따라서 sorting 이 NlogN보다 빠를 수 없기 때문에 최소 NlogN이 걸린다.
CCW (Counter-Clock-Wise)
좌회전
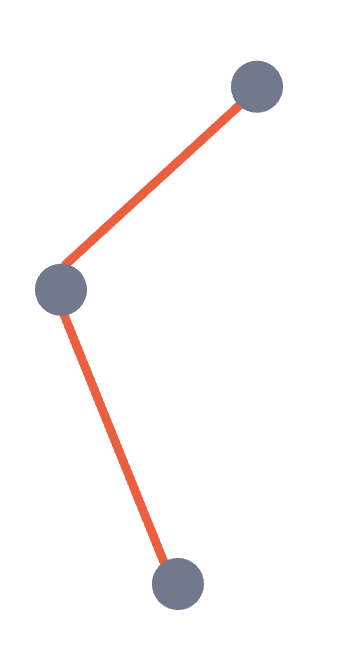

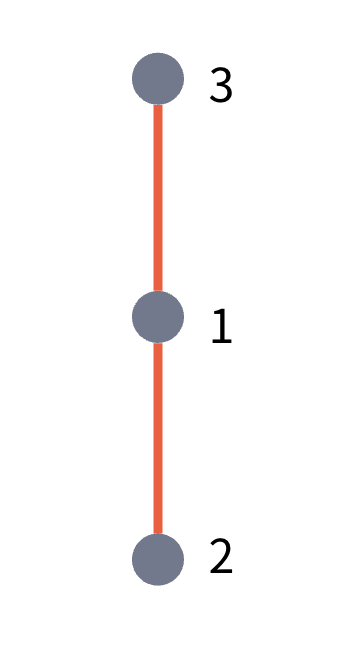
아래부터 (x1,y1) (x2,y2) (x3,y3)이라고 하자
지금 보는 그림은 우회전을 하는 그림이라 -로 나타날 것이다.
기울기를 보면 이가 좌회전인지 우회전인지 알 수 있다.
\(\frac{y_3-y_2}{x_3-x_2} - \frac{y_2-y_1}{x_2-x_1} > 0 \)이면 좌회전임을 알 수 있다.
앞에는 2,3의 기울기 뒤는 1,2의 기울이기다.
즉 기울기가 2,3의 기울기가 1,2의 기울기보다 크면
하지만 해당 식은 모든 경우에 사용할 수 없다. 분모가 0이 되는 등의 문제가 발생하기 때문
\((x_2 - x_1)(y_3-y_2) - (x_3 - x_2)(y_2 - y_1) = x_2y_3-x_2y_2-x_1-y_3+x_1y_2\)
\( = x_2y_3-x_2y_2-x_1y_3 + x_1y_2 - (x_3y_2 - x_3y_1 -x_2y_2+x_2y_1)\)
\( = x_1y_2-x_1y_3 + x_2y_2-x_2y_1+x_3y_1-x_3y_2 \)
\( = x_1(y_2-y_3) + x_2(y_3-y_1) + x_3(y1_y2)\)
특수 케이스의 경우 둘 다 0이 되기 때문에 구분이 어렵다 -> 좌회전도 우회전도 아님
멀어지는건지 가까워지는 것인지 따로 판단을 할 수밖에 없음
Brute-Force-ish 1
O(\(n^3\))의 시간이 걸린다.
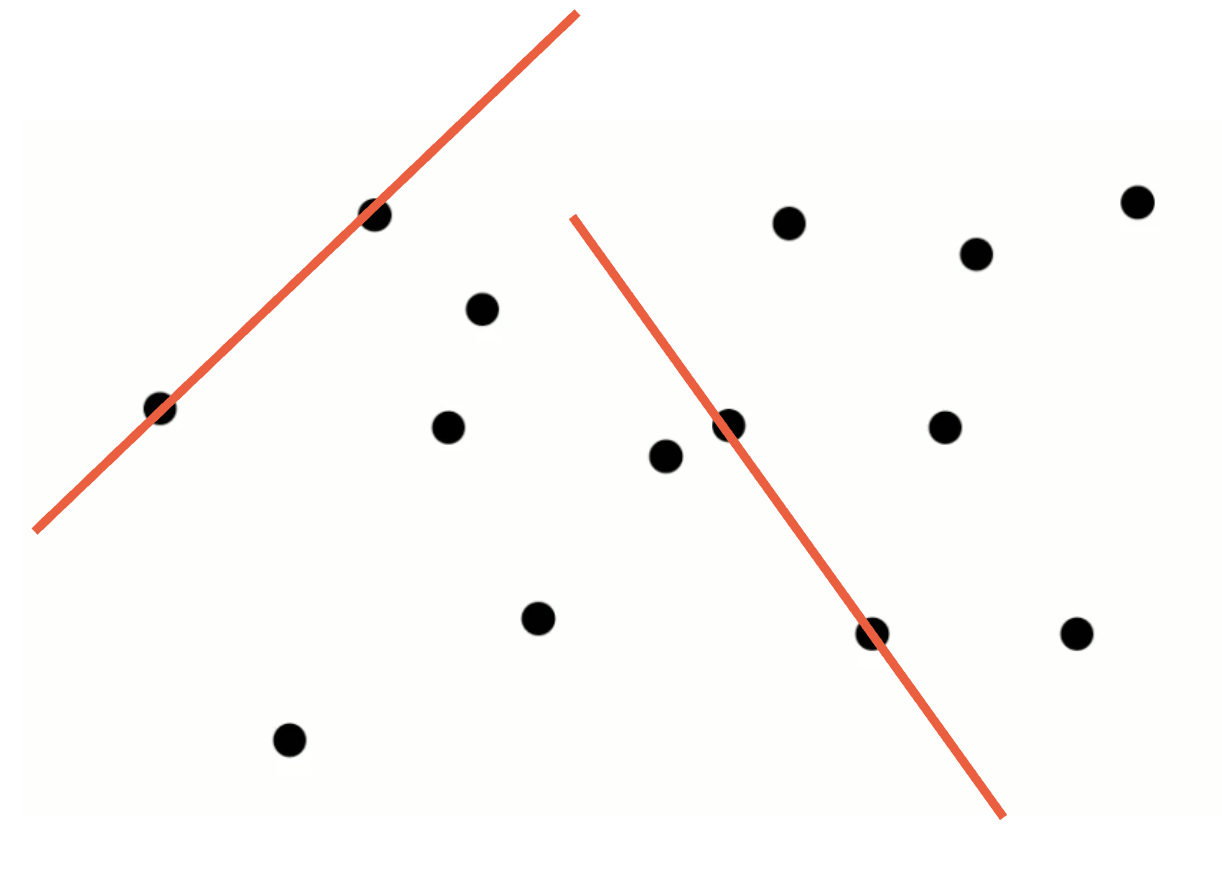
어떤 점을 가지고 만들 수 있는 선들이 있으면, 각 선분마다 그 선분이 convex hull 테두리인지 판단하는것이다.
내가 그린 한 선분을 쭉 직전으로 늘렸을 때, 한쪽에만 점이 있다면, convex hull의 테투리이다.
convex hull을 구했다고 치면, 모든 점이 다 한쪽에 있고 모든 점에 한쪽에 있다면 그것은 convex hull 테투리라는 필요충분조건을 만족
Brute-Froce-ish 2
O(\(n^2\)logn)
이것도 선분을 긋는데, 점을 중심으로 생각한다.
점에서 다른 점으로 선분을 그었는데, 180도 구간 내에서만 선분이 나가는 경우이다.
아무 선분도 없는 범위가 180도 이상일 때 convex hull의 꼭지점임을 알 수 있다.
각도로 sorting을 하면 중간에 180도를 넘어가는 것이 생길 것이다.
보통은 이것을 구현할 때 CCW로 구현한다.
그 중에서도, 가장 큰 각도로 벌어져 있는 두 선분이 테두리가 될 것이다.
Package Wrapping
O(\(n^2\))
sorting이 필요없다.
max or min을 구하면된다. 한쪽으로 쏠려있는것을 확인하는데 CCW로 쓴다.
maximum을 찾는 알고리즘과 같다.

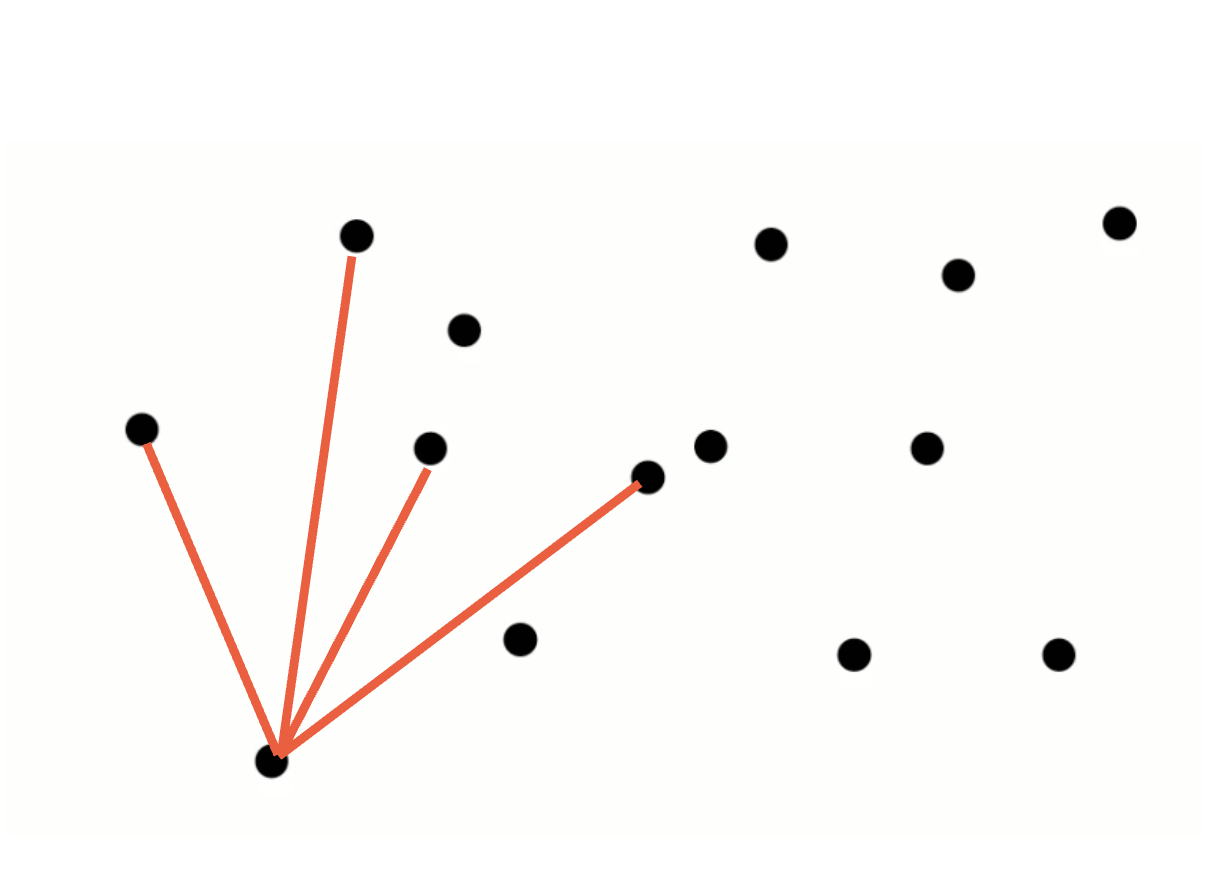
한 점을 기준으로 CCW로 좌회전인 것 즉, 맨 오른쪽에 있는 것을 찾는다.
한 점을 기준으로 하나씩 비교해가면서 하나를 기준으로 다음 번호에 연결한다. (그림처럼)
그러면, 현재 그림에서는 좌회전 하고 있으므로 먼저 잡은 점이 살아남는다. 그 다음 아무 점이나 차례대로 연결해나가며 맨 오른쪽 점을 찾으면 된다.
max를 찾는 알고리즘과 같다.
-> 따라서 sorting이 없어져서 조금 더 빨라진다.
Graham Scan
O(N log N) -> 상수도 작아서 가장 빠르다

이렇게 하나씩 선분으로 이어서 차례대로 선을 이었다고 생각하자
각도를 기준으로 sorting을 한다. (CCW로) -> 가장 오른쪽 것을 고른다.
여태까지 본 것들을 가지고 묵시적으로 convex hull을 만들었다. -> 아래 그림의 점선 같은 것
base) 지금까지 본것만 가지고 만들 수 있는 convex hull을 가지고 있다.
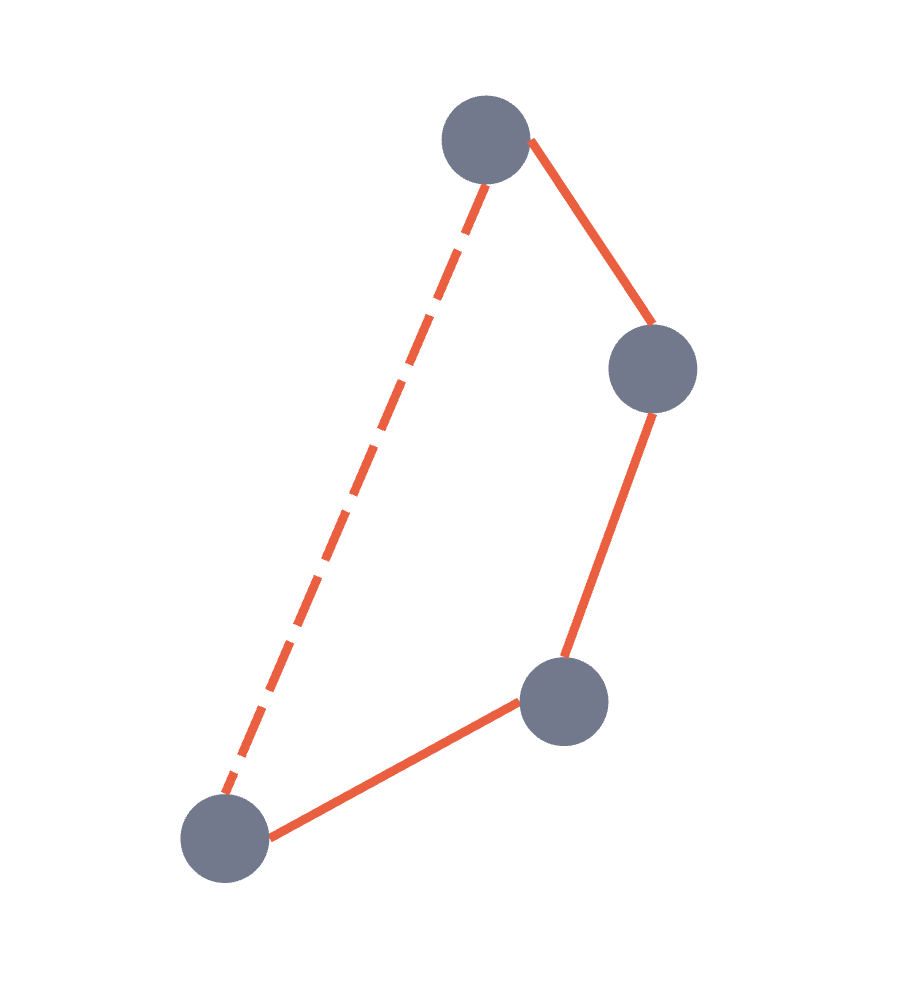


step) 지금까지 본 것들을 가지고 convex hull을 만들었다고 가정 -> 현재 k개의 점을 연결했다고 가정함
점들을 각도순으로 보고 있다. (왼쪽부터)
따라서, 현재 두번째 그림의 점선 사이에는 점이 없다.
* 묵시적으로 끝과 끝 점은 연결된다고 가정하면 convex hull 이 된다.
여태까지 본 점들의 convex hull을 만들 수 있다. -> 하지만 그것이 최종 convex hull아 아닐 수도 있음
stack에 지금 여태까지 본 점들의 convex hull의 점들을 저장한다. 그 중에서 최종 답에서는 여러개가 빠질 수도 있다
각도 순으로 다음 점을 본다.
1) 왼쪽에 점이 있는 경우
그림에서는 점선과 점선 사이에는 점이 없다. convex hull 밖에는 점이 없어야하는데, 현재 그 전의 convex hull 밖에는 점이 없기 때문이다.
직전에 본 것은 무조건 convex hull에 들어간다.
즉, 왼쪽인 경우 그냥 다른 점을 포함하면 된다.
2) 오른쪽에 점이 있는 경우
convex hull은 오른쪽으로 꺾이면 안된다. (볼록 다각형이여야하기 때문이다.
따라서 접선을 찾아서 그 부분에서 바로 오른쪽 부분으로 이어줘야한다.
현재 보면 왼쪽 -> 왼쪽 -> 왼쪽 -> 왼쪽 -> 오른쪽 이런식으로 꺾인다.
이따, 현재 연결되는 접선의 점을 기준은, 처음으로 "오른쪽 점"이 좌회전이 되는 부분이다. 그 다음 점은 우회전이 된다.
따라서 처음으로 좌회전이 되는 점에서 새로운 점을 추가해주면 된다.
스택에서 우회전이 된 점을 다 빼고 마지막 점을 스택에 추가해준다.
즉, 우회전이면 일부를 버리게 된다.
결국 스택에 따라가면서 좌회전을 확인하고, 우회전이라면 우회전을 만드는 것을 버리면서 스택에서 버리고 넣는다.
어떤 점이든지 들어가거나 / 남거나 / 버려진다.
점 하나를 봤을 때, 모든 점들은 상수 시간을 쓴다.
따라서 이를 스캔하는 부분은 O(N)이다.
Plane Sweeping
O(N log N)
Right Hull only
y좌표를 기준으로 생각한다.
convex hull이 있다면, left hull과 right hull 두 가지가 있다.
오른쪽 hull만 계산할 수 있다면 left hull도 반대로 계산하여 풀 수 있다.
sweep line이 지나간 부분에 대해서 right hull이 계산이 되어있다.

hull에 들어있는 점들만 B-tree에 들어있다.
다음 점이 들어왔을 때 해당 점을 추가로 반영하여 계산하면 된다.
새로 들어온 점을 기준으로 접선을 찾아서 계산하면 된다. (위쪽 접선과 아래쪽 접선을 구하면 됨)
접선을 찾고 나면 그 사이의 점들은 delete하면 된다.
-> 이러한 경우는 아주 위와 아주 아래에 점이 들어오는 경우까지 모두 생각하여 코딩해야함
만약, 맨 끝 점을 새로 들어온 점과 연결하면, 지금 있는 right hull을 뚫게 된다.
그려진 right hull에서, 맨 마지막 점에 수평으로 이어진 점이 있다고 가정하자.
해당 이어진 점을 "이전 점", 반대 방향을 "다음 점"이라고 할때 (현재 선분을 기준으로 왼쪽이 이전 점)
맨 마지막 점과 새로 들어온 점을 잇게 되면 CCW를 사용했을 때,
이전 점 대해서 좌회전, 다음 점에 대해서 우회전이라면 뚫고 나가는 점이 된다.
뚫고 나갔다면, 접점은 더 오른쪽에 존재한다.
만약 뚫고 들어간다면 목표점이 더 위에 있다 -> 바이너리 서치로 알 수 있음
Dynamic Case
점이 추가되거나 제거되는 경우 -> plane sweeping을 할 때 의미가 있다.
Convex hull을 만들 때, 점이 추가되는 등의 문제가 발생하면 배열을 다시 정렬해야하기 때문에 plane sweeping을 쓰면 tree 형태기 때문에 빠르게 할 수 있다.
Dynamic Case의 경우 Graham scan 이 잘 안됨
점이 제거될 때는 빠른 방법을 찾기 힘들다
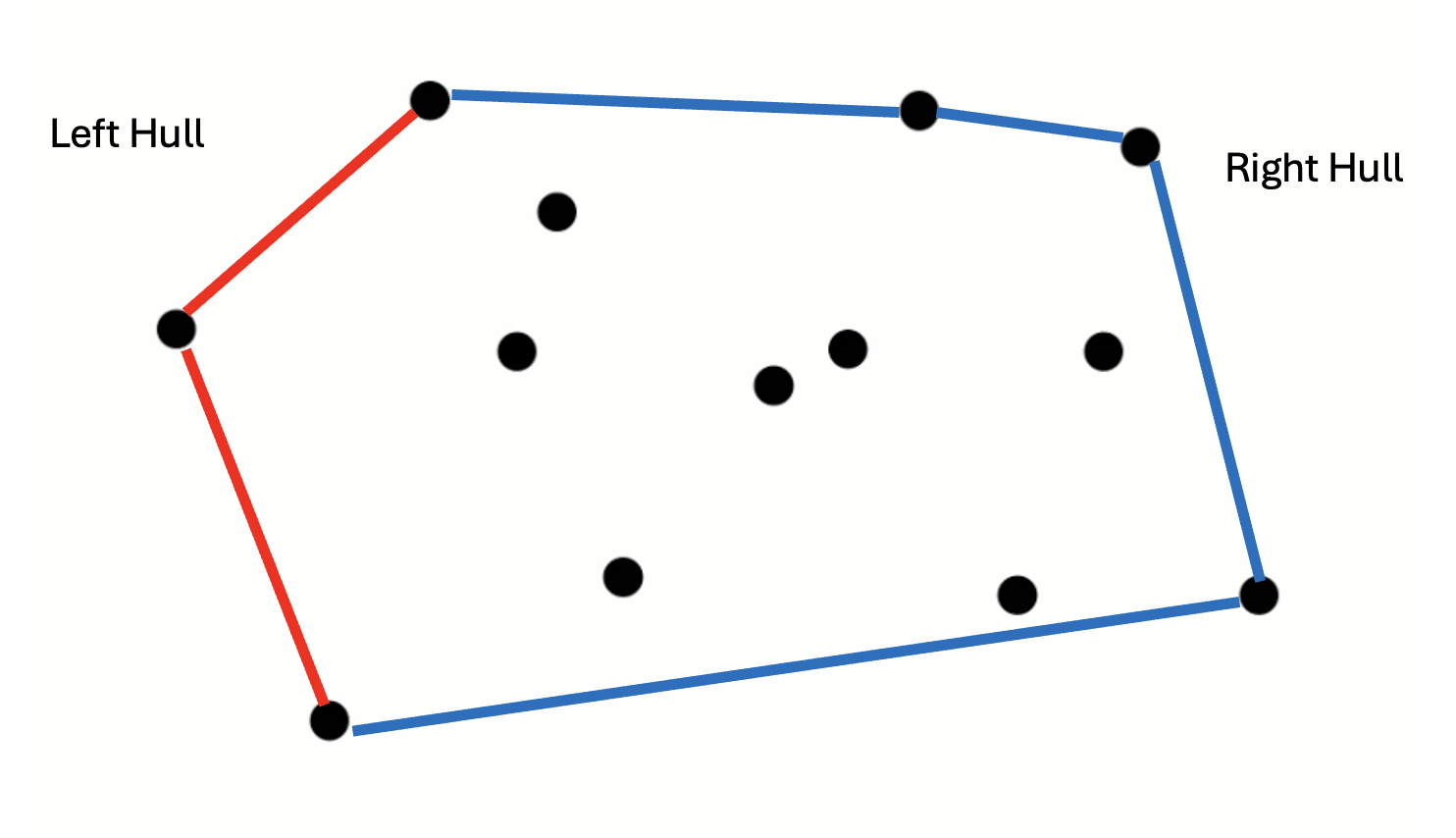
Plane Sweeping 방법으로 Left Hull 과 Right Hull을 구했다고 하자
배열이 아닌, Blance Tree에 현재 Hull을 이루는 점들이 들어있다.
만약 배열에 들어있으면 점들이 제거되고 추가될 때 inset와 delete가 오래 걸린다.
Tree 안에 y좌표 순서대로 들어있다.
점이 하나 추가되었다고 생각하자
추가된 점이 안쪽에 있는 경우
무시하면 됨
그렇다면 안쪽에 있다는 것을 어떻게 알 것인가?
Left Hull과 Right Hull이 따로 Tree에 저장되어있다.
그러면 새로 추가된 점의 y좌표를 기준으로 Left Hull의 Tree와 Right Hull의 Tree를 따라 내려가서 Left Hull과 Right Hull의 선분을 찾을 수 있음
즉 최고 y 좌표와 최저 y좌표가 있고, 이 사이에 있다면 알 수 있음
추가된 점이 밖에 있는 경우
밖에 있는 것을 Left hull과 right hull을 추가하여 할 수 있다.
-> Log N 정도 걸린다
Divide and Conquer
O(NlogN)
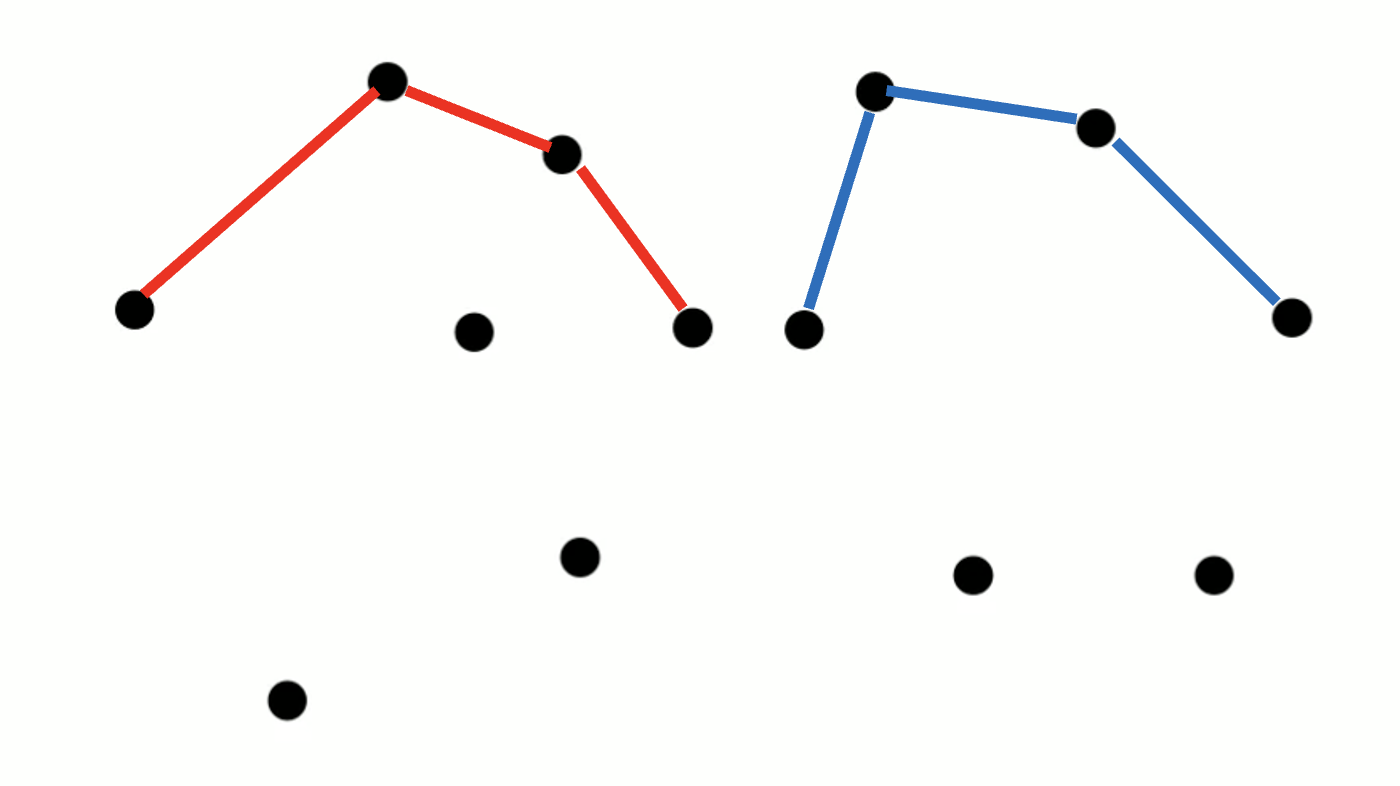
Upper Hull을 구한다.
왼쪽에서 Upper Hull, 오른쪽에서 Upper Hull을 각각 구한다.
양쪽의 공통 접선을 찾아, 나머지를 버린다
배열에 점들이 들어있다고 생각하자
왼쪽 아무 점에서 오른쪽 아무 점이나 찾아서 선을 긋는다.
잡은 왼쪽 점에서의 접점을 찾는다 -> 뚫고 나가는 것과 뚫고 들어오는 것과 관련하여 접점의 방향을 확인한다. (바이너리 서치)
이런 방식으로 해당 점의 접점을 찾을 수 있다.
이제 반대로, 해당 접점에서 왼쪽으로의 접점을 찾으면서 최종 공통 접선을 찾는다.
왼쪽과 오른쪽에서 각각 logN개의 점을 확인할 수 있으므로 O(log\(^2\)N)시간이 소요된다.
'CS > Algorithm' 카테고리의 다른 글
| [ Divide and Conquer ] Matrix Multiplication & Karatsuba Algorithm (0) | 2024.12.05 |
|---|---|
| [ Divide and Conquer ] Farthest Point (3) | 2024.12.04 |
| [ Divide and Conquer ] Closest Pair (3) | 2024.10.21 |
| [ Divide and Conquer ] The Selection Problem & Approximate Median (2) | 2024.10.20 |
| [ Divide and Conquer ] Recursive Merge Sort (0) | 2024.10.20 |