금화 모으기
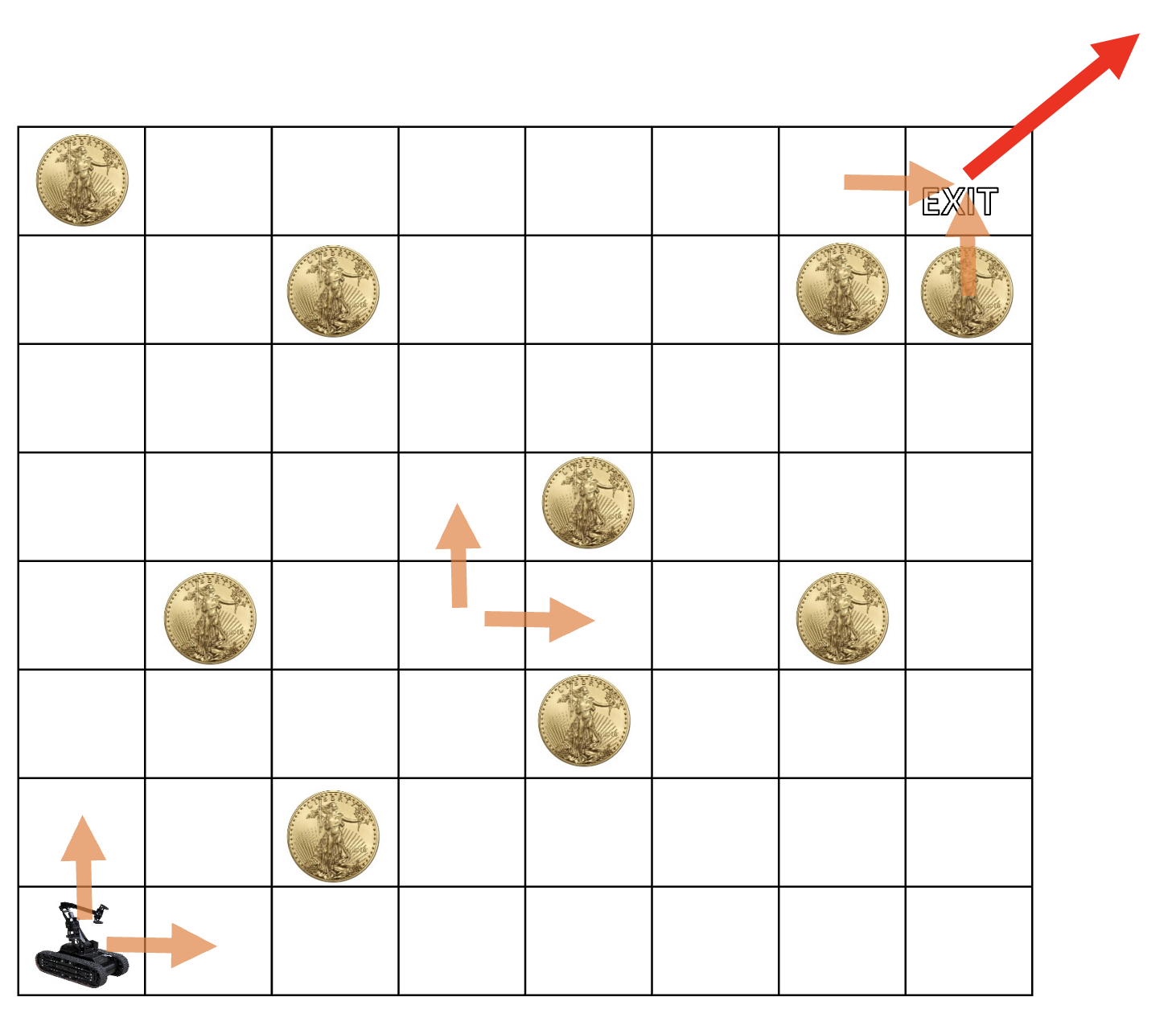

만약 연속으로 같은 방향으로 가지 못한다는 규칙이 있다고 생각하자
해당 칸에 왔을 때, 이전 방향을 기억하고 있어야한다
결국, 중간 부분에서 왼쪽에서 오는 것인지 아래에서 오는 두 가지 모두 알고 있어야한다
결국 과거 일을 덜 기억해야할 수록 더 쉽다
로봇이 (i,j)에 도착할 때까지 모을 수 있는 최대 금화 개수

Pseudo Polynomial 설명
pseudo polynomial 이라는 알고리즘들 중 하나이다.
어떤 입력이 n일 때 O(\(n^2\))이 걸린다.
n개의 숫자가 얼마나 큰지 작은지에 상관 없이 우리는 항상 n이라고 생각한다. 작은 값들과 큰 값들은 연산에 차이를 보인다
사실은 비트 수에 따라서 비교를 해야하기 때문에 엄청나게 큰 숫자는 작은 숫자와 연산에 차이가 있다
즉, 비교하는데에 걸리는 시간을 1로 두기 때문에 NlogN이라고 해도, 비트 단위로 생각해야함
주어진 값이 작냐 크냐에 따라서도 달라진다
n -> 실제 입력 사이즈(bit) O(logn)이다
\(n^2\) = \(2^{2logn}\)
즉 O(n^2)은 보기엔 polynomial처럼 보이지만, 지수 시간이 걸리는 것이다.
그래서 pseudo polynomial이라고 하는 것이다. polynomial처럼 보이기 때문에
동전 거스름 돈
N 원의 거스름 돈을 돌려 줄 때, 최소 갯수의 동전을 사용하여 거스름돈을 돌려주는 방법을 구하시오. 동전의 종류는 1원, 4원, 6원
에를 들어 8원을 거슬러주려한다.
그리디 방법 (가장 큰 단위 동전 사용)을 이용한 접근 : 6원, 1원, 1원 => 동전 3개
최적 : 4원 동전 2개
따라서 그리디 방법으로 구하기 어렵다. 동적 계획법으로 해결하자
재귀 알고리즘
1원 동전 한 개 + 7원에 대한 최적해
4원 동전 한 개 + 4원에 대한 최적해
6원 동전 한 개 + 2원에 대한 최적해
위의 3가지 해 중 최적해를 선택
7원에 대한 최적해는 다시 1,4,6원 선택하고 나머지 액수에 대한 최적해를 구한다
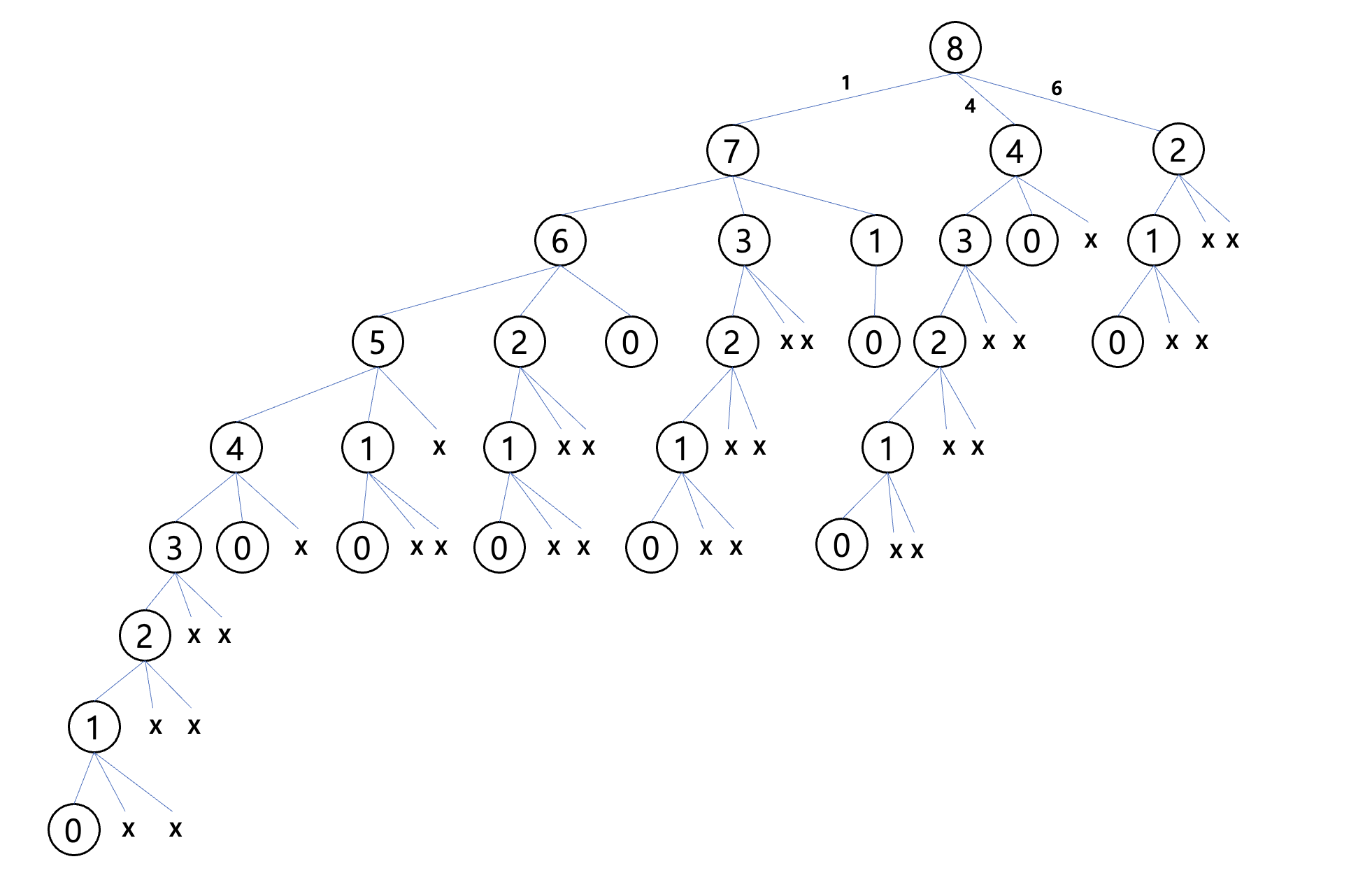
이런식으로 호출하는 tree를 확인할 수 있다.
중복 (overlapping subproblem)이 발생하기 때문에 시간이 오래 걸리게 된다.
방법 1 DP : 상향식
1원에 대한 최적해 -> (선택) -> 2원에 대한 최적해 -> (선택) -> 3원에 대한 최적해 ...
C[j] = j원을 거슬러 줄 때의 최적
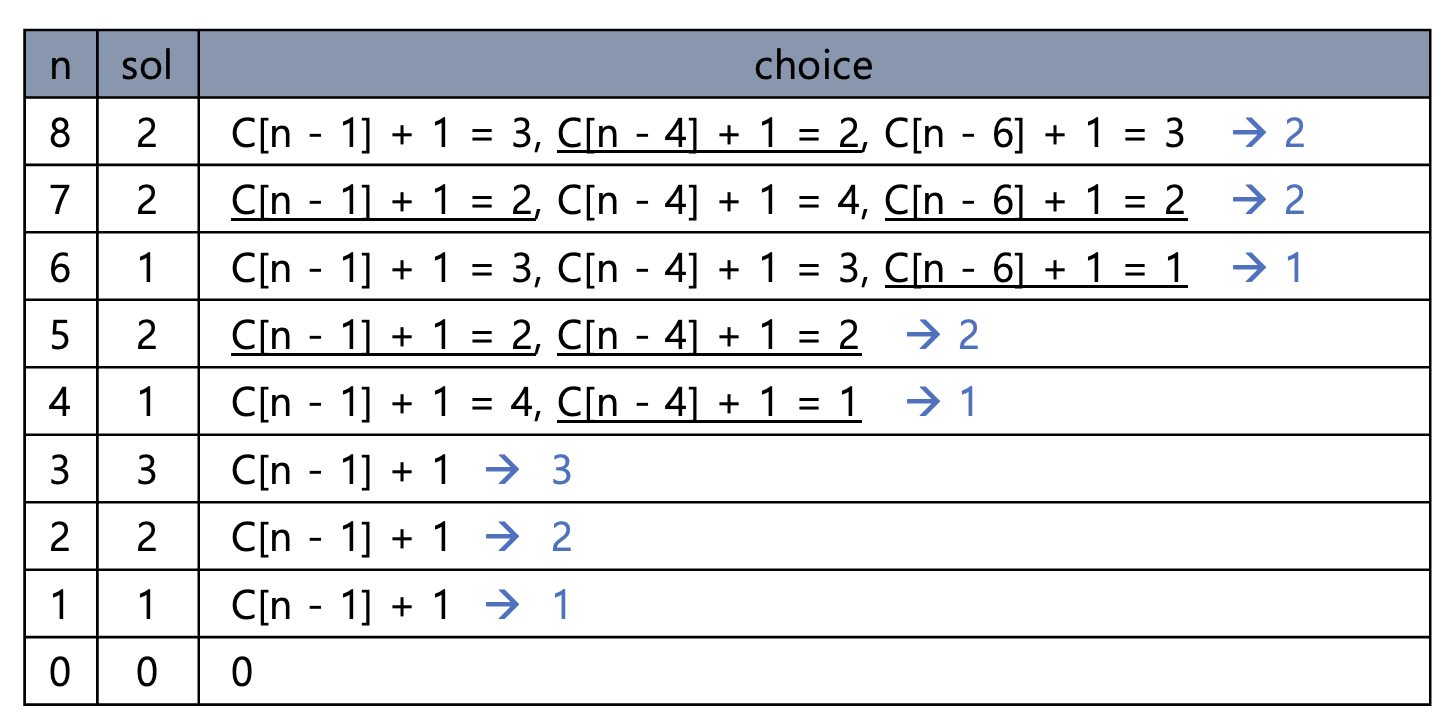
방법 2 DP
부분 문제 정의
C(i,j) = 최대 크기 Di 동전으로 j원을 거슬러 줄 때의 최적
- (D1 는 1원 D2는 4원 D3은 6원)
- 거스름 돈에 (1) Di 동전을 사용한 경우, (2) 사용하지 않은 경우
최적화 원리 : 만약 최대 크기 Di 동전으로 j원을 거슬러 줄 때 최적으로 거슬러주지 않는다면, 전체 문제의 거스름돈의 개수도 최적이 되지 않는다.
C(i,j) = min{ C(i,j-Di) + 1, C(i-1,j)} -> O(i*j)
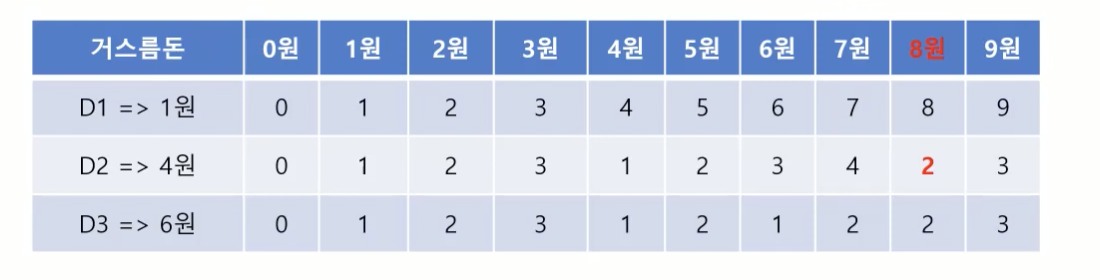
표에서는 그것을 쓰던 안쓰던 가장 좋은것을 쓴다
프리랜서의 일정 정하기
프리랜서에게 10일간의 작업에 대한 요청이 있다. 각 작업의 기간과 수당은 아래와 같다. 하나의 작업을 하는 동안 다른 작업은 할 수가 없다. 주어진 일정에서 수당의 합이 가장 크도록 작업을 선택하시오

greedy 하게 실행한다면 T3를 선택해야하지만, T3가 다른 모든 일정과 겹치기 때문에 다른 일정을 선택할 수 없다.
하지만 T1 + T7을 선택하면 더 많은 수당을 받을 수 있다.
부분 문제들 OPT (j)를 정의한다
각 작업이 마치는 시간을 key로 하여 전체 작업을 다시 정렬하고 순서대로 번호를 붙인다.
즉, 작업 j는 전체 작업 중 j번째로 마치는 작업이다.
OPT(j) : 1부터 j 까지의 작업에 대한 최적의 해
OPT가 작업 j를 선택하지 않음 : OPT(j) = OPT(j-1)
OPT가 작업 j를 선택함 : OPT(j) = w(j) + OPT(p(j))
- p(j)는 작업 j와 겹치지 않고 p(j) < j 인 작업들 가운데 맨 마지막 작업
- W(j)는 작업 j를 수행했을 때 받은 돈 액수
OPT(j) = max {OPT(j-1), w(j) + OPT(p(j))}
집합에서 k개 선택하기
N개의 원소로 구성된 집합 {1,2,3,4,5,6,7,8,9,10}에서 서로 다른 k개를 순서 없이 선택하는 방법은 모두 몇개인지 구하시오
* K = 4일 경우, {1,2,3,4} {4,8,9,10} ...
DP 접근
만약 답이 존재한다면 그 답은 경우들로 나누어지는지 생각해보자
크기 4의 부분집합 {a,b,c,d}이 있다면 그것은 2가지로 나눠볼 수 있다.
Case a) 1을 포함하는 것
Case b) 1을 포함하지 않는 것
n'(<n)개의 서로 다른 k'(<=k)개를 선택하는 부분 집합들의 개수를 구하는 문제들에 대해 답을 알고 있다고 하자
n개에서 선택한 크기 k개의 부분 집합은 두가지 경우에 속한다
- Case a) 1을 포함하는 부분 집합들 : 1을 제외한 n-1개에서 k-1개를 선택한 부분 집합들에 1을 추가
- Case b) 1을 포함하지 않는 부분 집합들 : 1을 제외한 n-1개에서 k개를 선택한 부분 집합들
전체 답은 Case a) + Case b)
C(n,k) = C(n-1,k-1) + C(n-1,k)
=> 파스칼 삼각형
숫자판 놀이
칸마다 숫자가 적힌 배열이 주어져 있다. 위에서 아래로 내려가면서 지나는 숫자만큼의 상금을 받는다. 단 움직이는 방향은 양쪽으로 최대 1칸씩만 허용한다. 가장 돈을 많이 받을 수 있는 이동 방법을 구하시오
Cell에 도착하는 방법은 왼쪽위, 위, 오른쪽 위 세 가지 방향이다
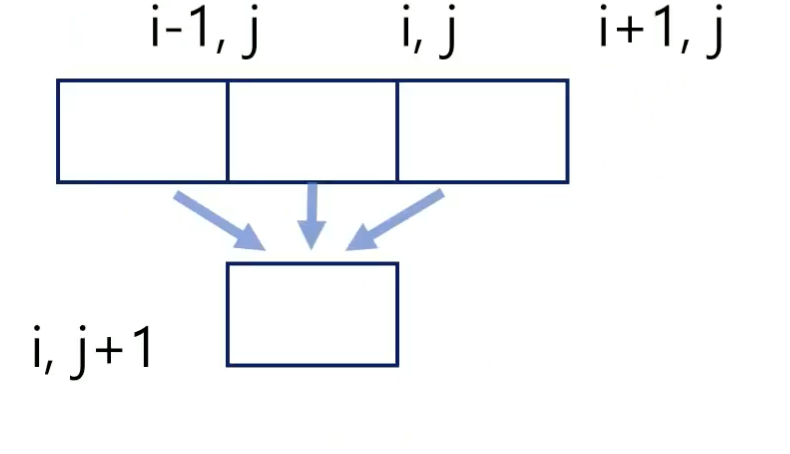
Sum(i, j+1) = max { Sum(i-1, j), Sum(i,j), Sum(i+1,j) } + Cell[i,j+1]
Longest Increasing Subsequence
가장 긴 증가하는 subsequence를 찾는 문제
- Find the LIS ending at element i, for each i
- N^2 is easy (DP)
C[i] = i번째를 마지막으로 가지는 increasing Subsequence의 갯수
만약 N이 10만이 넘어가게 된다면, N^2으로 풀 수 없다.
따라서 O(NlogN)으로 해결해야한다
1) 세그먼트 트리 이용
자기 이전의 값을 찾아 읽는데에 logN 시간이 걸리게 되므로 NlogN에 가능하다
2) 이진 탐색을 이용하여 최적의 위치에 수를 삽입하는 방식
만약, 어떤 벡터가 있다고 가정하자
해당 벡터에 -INF가 있고
차례대로 수열을 읽어나가며 벡터에 있는 마지막값보다 크면 벡터에 넣는다.
만약 벡터에 있는 값이 더 크다면, lower bound부터 찾아 바꾸어준다.
완전 정보 게임 (NIM Game)
- 게임의 정보가 참가자 모두에게 공개된 게임
- 숨어있는 정보는 없다.
- 누가 먼저 하는가에 다라서 승부는 이미 결정되어 있다. (양쪽이 최선을 다한다면 -> 상대방의 수에 관계없이 내가 이길 수 있음)
- ex) 바둑, 오목, 체스 등
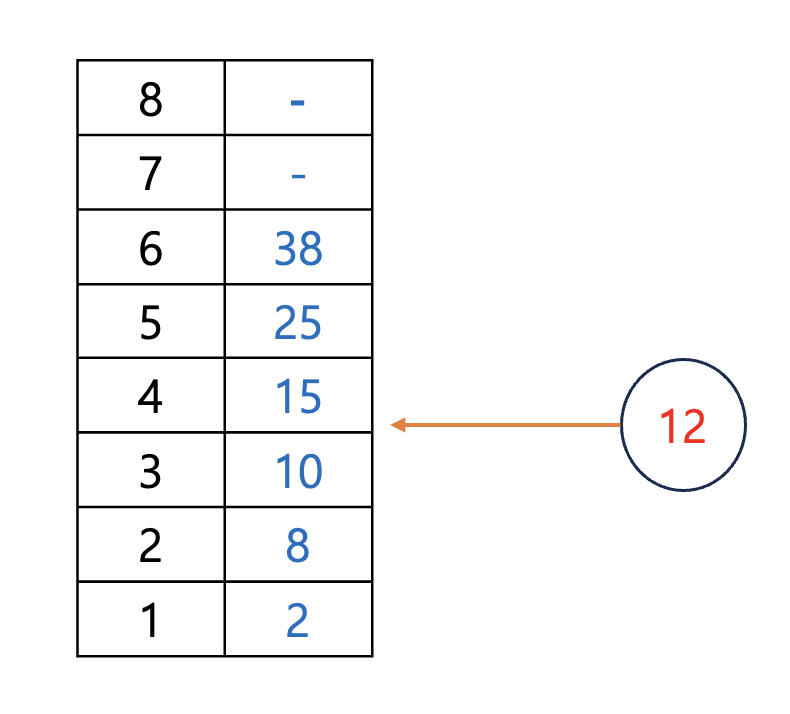
바둑돌 가져가기 1
바둑돌이 K개 있다. 두 사람이 번갈아가며 자신의 차례에 1개, 2개의 돌을 가져갈 수 있다. 자신의 차례에 동작을 할 수 없으면 그 사람이 진다. 이기는 방법이 있는 사람과 그 사람이 이기는 방법을 구하시오
부분 문제 D(i) : 돌의 갯수가 i개 일 때, 이기는 방법이 있는 경우
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| X | O | O | X | O | O | X | O | O | X |
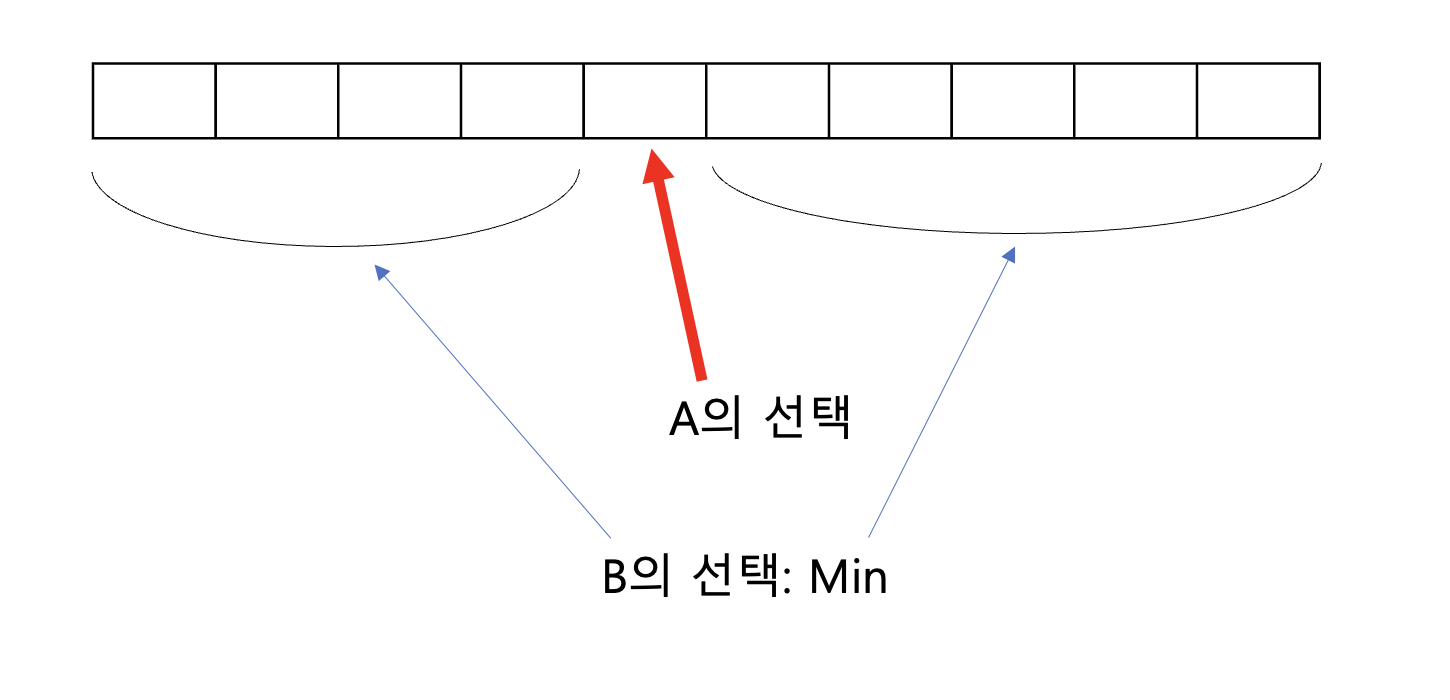
돌 가져가기
- N piles of Stones, Number of Stones in each Pile known
- Two players A and B
- A takes one pile X
- B takes all of either left or right of X
- Repeat
- What is the maximum score A can guarantee? (최선을 다한다면)
N^3 : Compute score for all consecutive Subsequence
A가 k번째 수를 가져가면, B는 더 작은 합이 남아있는 쪽을 고른다 (더 큰 값인 쪽을 없앰)
A가 몇점을 가질 수 있을 지 알려면 오른쪽과 왼쪽의 점수를 알아야한다 -> 작은 것들의 점수를 알면 큰 것의 점수를 알 수 있음
size가 1인 경우, 해당 돌을 가져가면 됨
size가 2인 경우, 둘 중 큰 것을 가져가념 됨
... 이런식으로 반복하여 n까지 가게 되면 n^3 알고리즘이 되게 된다.
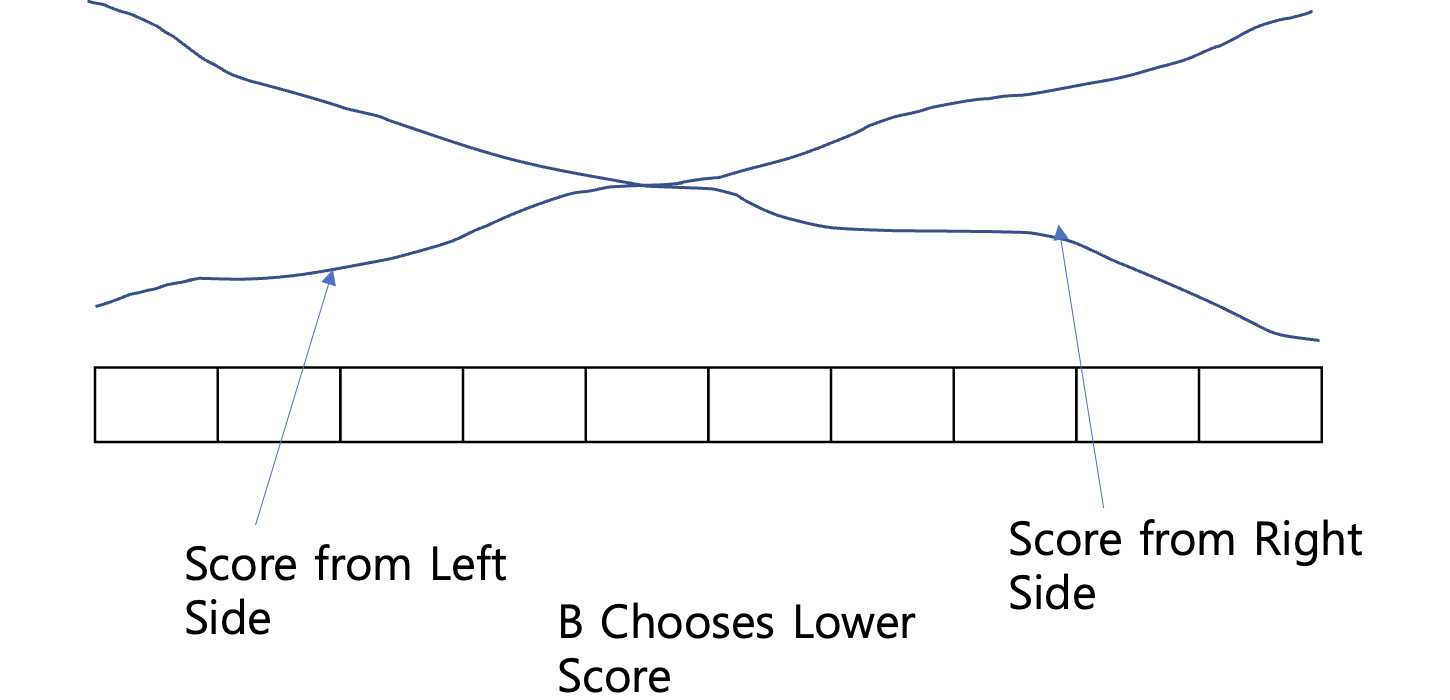
해당 10개에서 dp를 계산했다고 생각하자.
이때, 다음 값이 추가되면 저 최선의 선택인 교점은 무조건 오른쪽으로만 움직이게 된다.
따라서 몇 칸 옆으로 가는게 늘어난 것보다 많이 움직이지 못하므로 N^2 시간에 계산할 수 있다.
'CS > Algorithm' 카테고리의 다른 글
| [Graph Traversal] DFS Tree (0) | 2024.12.10 |
|---|---|
| [Graph Traversal] Any-order Traversal & Connected Component & Event Queue & RDFS (1) | 2024.12.09 |
| [Dynamic Programming] Sequence Alignment & 최대 공백 정사각형 (0) | 2024.12.09 |
| [Dynamic Programming] 근사 문자열 매칭과 거리 함수 & LCS (0) | 2024.12.09 |
| [Dynamic Programming] Working Days & Path Counting & Matrix Chain Multiplication (0) | 2024.12.09 |