DFS Tree
전진(재귀 호출)을 한 edge로 만듦
- DFS Tree is the Result of DFS
- Usually analyze DFS Tree to get information
DFS Tree에 있는 edge를 Tree edge라고 부른다
그리고 Tree edge에 포함되지 않은 것들을 Back Edges라고 한다
- Edges of input Graph becomes Tree or Back edges of DFS Tree
Back edges는 전부 자손과 조상을 연결하는 것 밖에 없다
그 이유는, 조상이 아닌 다른 것과 연결되어 있었다면, 아래로 호출했을 것이다.

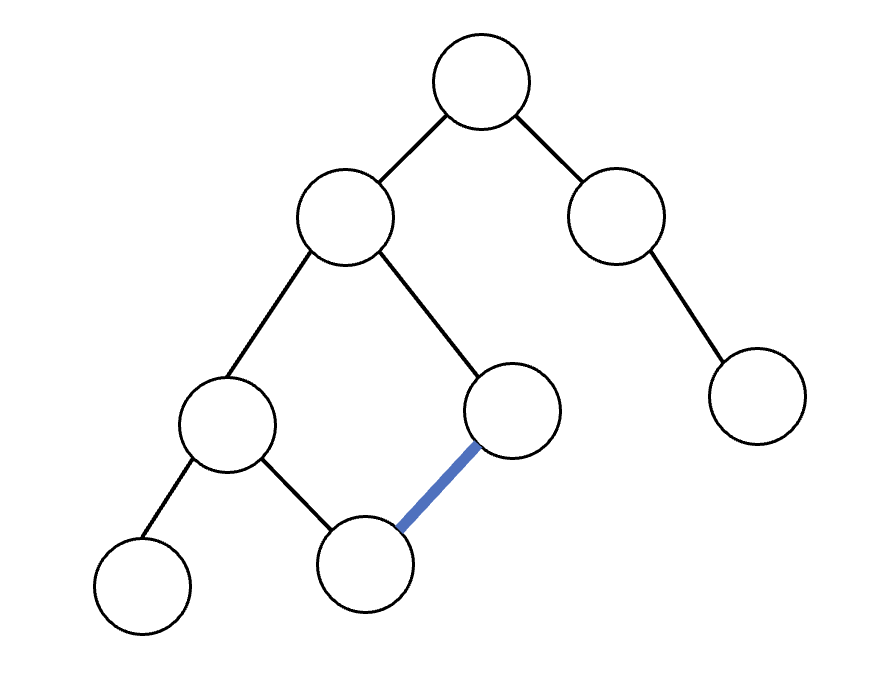
파란색 선을 back edge라고 가정한다면
이미 노드가 연결되어있다는 것이다.
그렇가면, 만약 맨 아래 leaf가 DFS를 통해 저 노드를 호출할 수 있었을 것이다.
하지만 호출되지 못했다는 것은 연결되어있지 않다는 뜻이다
따라서 back edge는 이미 연결되어있던 자신의 조상에게로만 연결될 수 있다.
즉 back edge는 이미 마킹한 것이므로 뒤를 돌아본다고 해서 back edge라고 하는 것이다.
따라서 저런 Cross edge는 불가능하다
Bipartite Graph Detection
bipartite라는 증거가 하나만 있으면 가능하다
DFS Tree를 만든다.
Tree edge만 봐도 bipartite를 확인할 수 있다
두 집합 A,B가 있다고 가정하자

Tree edge만 봤을 때 어디에 속해야하는지 확인할 수 있다
어떤 DFS를 하더라도 무조건 저 방법이 적용된다
그 이후로 back edge를 확인을 하는데, 같은 그룹끼리 연결된 back edge가 없으면 bipartite graph라는 것을 확인할 수 있다
Tree edge와 Back edge는 미리 정해져있는 것이 아니라 DFS를 하면 정해지게 되는 것이다.
그래프 특징만 가지고 나오는 것이 아니라 트리를 활용하여
'CS > Algorithm' 카테고리의 다른 글
| BCC (0) | 2024.12.11 |
|---|---|
| [Graph Traversal] Cut Vertex (0) | 2024.12.10 |
| [Graph Traversal] Any-order Traversal & Connected Component & Event Queue & RDFS (1) | 2024.12.09 |
| [Dynamic Programming] 문제 모음 (0) | 2024.12.09 |
| [Dynamic Programming] Sequence Alignment & 최대 공백 정사각형 (0) | 2024.12.09 |