Def Cut Vertex
- Removing a node s makes Graph Disconnected
- Exists x and y s.t., all paths from x to y goes through s : 노드 x, y가 있어서 x, y를 연결하는 모든 path가 s를 지나감
연결된 그래프에서만 생각한다
연결된 그래프에서 특정 노드를 지우면 끊어진 그래프가 될 때 그 노드를 cut vertex라고 한다
- G = (V,E)
- |V| = n, |E| = m
- undirected graph
(=>) 노드 S를 제거하면 Connected component가 여러개 생김
서로 다른 connected component 에서 x, y라는 노드를 각각 고름
이러면 x, y 로 통하는 path 가 없다. 따라서 현재 s를 제거하면서 이 두개를 연결하는 path 가 없어진 것이다
(<=) x에서 y로 가는 path가 어려개 있는데 전부 s를 통해서 감 (한 쌍이라도 있으면 됨)
s가 사라지면 x, y 사이의 path가 사라지고 disconnected 됨
따라서 cut vertex를 풀고 싶다
우리는 Connected Components를 찾을 수 있다
정의에 따라 문제를 해결하기 위해 Graph에서 노드를 지우고 Connected Components를 찾아 그 갯수를 세면 된다
O(mn)의 시간이 걸리게 된다
Cut Vertex
- Run DFS(O(m+n)), Build DFS Tree
- Root of DFS Tree is a Cut Vertex iff it has more than 1 child : child가 1개가 넘으면 무조건 cut vertex이다
만약 child가 1개라면
Root 노드 R을 지운다고 하더라도 모두 연결되어있다. back edge가 물론 존재하지만, Tree edge만 본다고 하더라도
만약 child가 2개 이상이라면

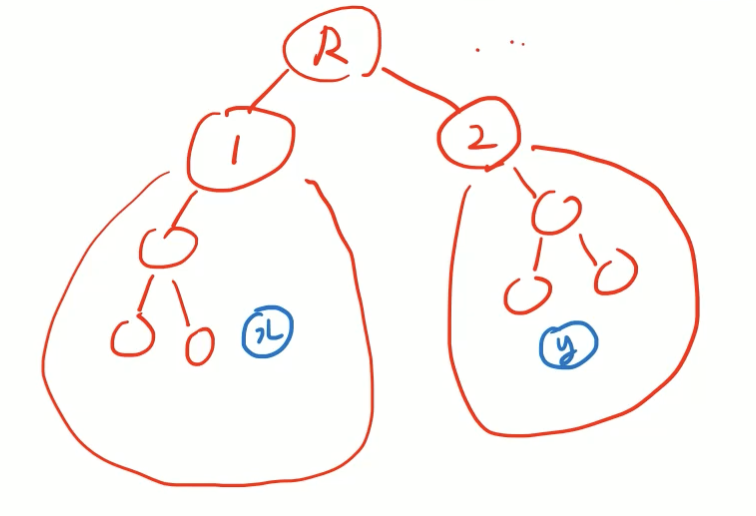
또 다른 sub tree가 물론 존재할 수 있음
1번 노드 아래에 아무 노드나 x, 2번 노드 아래에 아무 노드나 y로 한다
x, y를 잇는 모든 path는 R을 지나가게 된다
x에서 R을 안가고 Tree edge만 쓰면 1번 구역을 벗어날 수 없다. 즉 R을 반드시 거치게 된다
back edge를 확인해야한다. 하지만, back edge는 조상과 자손을 잇는 방법밖에 없다
조상 중 가장 높은 것은 1번 or R이다.
1번으로 가더라도 subtree이고, R로 가더라도 결국 R을 지나게 되는 것이다
이렇게 되면 새로운 알고리즘을 생각할 수 있다
For Each Node s, Run DFS from s (to make it the Root) and check if s is a Cut Vertex
결국 모든 노드를 root라고 생각하면서 DFS를 돌린 후, subtree의 갯수를 확인해야한다.
=> O(mn)
이 방법이 어렵기 때문에
DFS를 한 번 돌리고 Cut Vertex를 판단하는 방법이 있어야할 것 같다
다시 정의를 보자
Root of DFS Tree is a Cut Vertex iff it has more than 1 child이다
만약 Non-Root Node t에 대해서는 어떠한가?
- For each t computae l(t), which is the minimum of
- Pre(t) : DFS를 하면서 노드에 붙인 번호 (Root가 1번, 왼쪽 노드부터 들어간다. -> 위로 올라가면 작아진다)
- Min of Pre(s) where (t,s) is a Back Edge (Back Edge의 연결된 더 작은 번호 -> 조상의 번호)
- Min of l(u) for all children of t (Child의 l값 -> child에서 올라갈 수 있는 번호)
결국 의미는 t에서 l값이라는 것은 sub tree를 돌아다니다가 back edge를 한번만 타고 갈 수 있는 가장 높은 것이다
t is a Cut Vertex iff exist a child u of t, s.t., l(u) >= Pre(t)
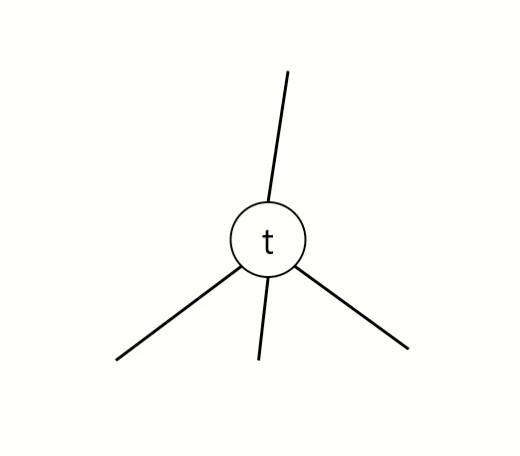
child 중에 back edge를 타고 t까지 밖에 오지 못하는 child 가 있으면 t가 Cut Vertex이다
나와 내 child의 관계를 따져야한다.
Proof
child u가 존재, l(u) ≥ Pre(t) <=> t, a cut vertex

node x와 node y가 있어서 x, y 의 path가 모두 t를 지난다는 정의를 사용하자
x가 있는 서브트리의 가장 위 노드를 u라고 하자
u의 서브트리에 y가 없다. 결국 x는 u의 서브트리에서 나가야한다
tree edge를 써서는 무조건 t를 거쳐서 u의 서브트리를 벗어날 수 있다
back edge를 거치고자한다 -> back edge를 타도 서브트리를 벗어나는 순간 t이다
저러한 child가 없다면 모든 child에 대해서 t위로 올라갈 수 있다.
그렇게 되면 t를 빼도 전부 연결되어있다
즉 저 조건을 만족하지 않는다는 것은 cut vertex가 존재하지 않는다는 것이다
Time
- Root of DFS Tree is a Cut Vertex iff it has more than 1 child -> O(m+n) for DFS
- Non-Root Node t?
- For each t compute l(t), which is the minimum of
- Pre(t) -> DFS 하면서 계산
- Min of Pre(s) where (t,s) is a Back Edge
- Min of l(u) for all children of t -> DFS 다시 돌림 post order 계산
- t is a Cut Vertex iff exist a child u of t, s.t. l(u)>= Pre(t)
결국 O(m+n)
Cut Edge
edge를 끊어서 disconnected로 만들 수 있는 것
edge 사이에 node가 있다고 생각하자
그러면 새로운 그래프가 나오게 된다
G' = (V,E)
node 갯수 : m +n
edge 갯수 : 2m
'CS > Algorithm' 카테고리의 다른 글
| Topological Sort (0) | 2024.12.11 |
|---|---|
| BCC (0) | 2024.12.11 |
| [Graph Traversal] DFS Tree (0) | 2024.12.10 |
| [Graph Traversal] Any-order Traversal & Connected Component & Event Queue & RDFS (1) | 2024.12.09 |
| [Dynamic Programming] 문제 모음 (0) | 2024.12.09 |