Routing Algorithm
Routing Algorithm : 루트를 결정하는 알고리즘 (Host-to-Host) & algorithm that finds that least cost path
Graph G = (N, E)
N = set of Nodes (ROUTER)
E = set of Links
Cost = 여러 상황을 고려하여 링크에 부여되는 값으로, 한 라우터에 많은 부담이 생기면 바뀔 수 있음
cost는 물리적인 거리만 고려한 것은 아니다
라우터를 거치지 않는 것이 더 적은 cost가 드는 것은 아니다.

파란색은 cost가 5, 빨간색은 cost가 4이기 때문에 결국 빨간 경로가 cost가 더 작다.
c(x,y) or \(C_{xy}\) : 둘 다 x,y의 cost를 나타낸다.
If (x,y) \(\notin\) E -> \(C_{xy}\) = +∞ : 만약 x,y 사이에 링크가 존재하지 않는다면 무한대로 둔다.
결과적으로 cost가 작은 값을 구해야함
- A graph is Connected if there exists a path between every pair of nodes
- Find the shortest path from a given node to every other node
*일반적으로 host는 하나의 라우터에 연결되어있다
이때 그 라우터를 default router라고 한다
Optimality principle
Cost 가 가장 적은 path를 찾는 것
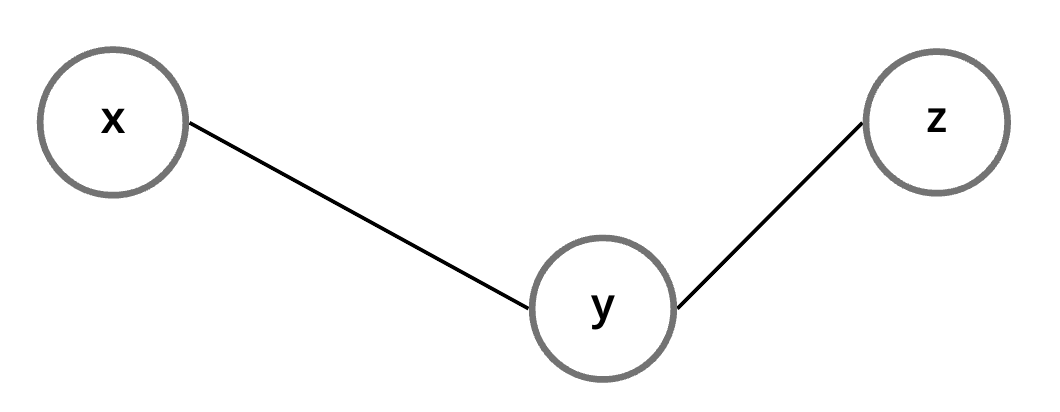
x - z가 shortest 이고 (cost가 가장 작다)
x - y가 shortest 이면
y - z도 shortest 이다.
Link state vs Distance vector
Link state : use global information : 모든 path의 cost(정보)를 알고 있다.
Distance vector : Decentralized and iterative process 연결된 링크의 정보만 안다.
global vs decentralize
global : all routers have complete info about topology(전체 노드들이 어떤식으로 연결되어 있는지에 관한 모양)
-> link stat algoithms
decentralize : router knows physically-connected neighbors, link costs to neighbors
이웃 노드들에 관한 정보들만 알고 있다.
-> distance vector algorithms
Static vs dynamic
statkc : routes change slowly over time 상태 변화를 천천히 업데이트 -> 정확한 상태 파악 불가
dynamic : routes change more quickly 상태 변화를 주기적으로 업데이트 -> 변경 정보가 필요하기 때문에 overhead 커짐
Dijkstra's Algorithm
=> Link-State routing Algorithm
- net topology, link costs known to all nodes : 링크 토플로지와 cost가 전부 알려져있다
- accomplished via "link state broadcast"
- all nodes have same info
- computes least cost path from one node ('source') to all other nodes (forwarding table)
- iterative : after k iterations, know leask cost path to k dest.' s
C(x,y) : link cost from node x to y
D(v) : current value of cost of path from source to dest
p(v) : predecessor node along path from source to v : 연결된 직전 노드
N' : set of nodes whose least cost path definitively known
Example

u부터 z까지 가는데에 optimal 한 path를 찾자
| STEP | N' | D(v) / p(v) | D(w) / p(w) | D(x) / p(x) | D(y) / p(y) | D(z) / p(z) |
| 0 | u | (7,u) | (3,u) | (5,u) | ∞ | ∞ |
| 1 | u, w | (6,w) | (5,u) | (11,w) | ∞ | |
| 2 | uwx | (6,w) | (11,2) | (14,x) | ||
| 3 | uwxv | (10,v) | (144,x) | |||
| 4 | uwxvy | (12,y) | ||||
| 5 | uwxvyz |
∞ : 연결이 (직접적으로) 되어있지 않다. 정확히는 현재까지 본 노드들과 바로 연결되어 있지 않다.
- 가장 작은 cost를 가진 노드를 N'(현재까지 본 노드의 set)에 넣는다 -> 답으로 확정한다
- 최종 목적은 u-z의 최적 경로지만 그 과정에서 모든 노드로의 최적 경로도 알 수 있다.
- 노드를 연결하면서 이웃들 (direct)연결을 update한다
- ex) D(y) = min(11, D(v) + c (v,y)) = D(v) + C(v,y) = 10
- 최적의 path를 구할 수 있음 (이전 노드를 참고하자)
- 만약 최소 값이 2개일 때는 어떤 것을 먼저하든지 상관 없다

| STEP | N' | D(B), P(B) | D(C), P(C) | D(D), P(D) | D(E), P(E) | D(F), P(F) |
| 0 | A | (2,A) | (5,A) | (1,A) | ∞ | ∞ |
| 1 | A,D | (2,A) | (4,D) | (2,D) | ∞ | |
| 2 | A,D,B | (3,E) | (2,D) | ∞ | ||
| 3 | A,D,B,E | (3,E) | (4,E) | |||
| 4 | A,B,C,D,E | (4,E) | ||||
| 5 | A,B,C,D,E,F |
B와 E 중 무엇을 먼저 추가해도 상관 없다
A를 기준으로 1,2번 (cost 그대로) Link의 번호라고 가정하자
A에서 dest가 어떤 노드일 때 forwarding table을 작성해보자
| dest | link |
| B | 2 |
| C | 1 |
| D | 1 |
| E | 1 |
| F | 1 |
Dijkstra's algorithm, discussion
우리는 지금까지 다익스트라의 가정을 link 사이의 cost가 패킷의 트래픽과 동일하다고 가정했다.
즉, cost가 고정되어있다.
direction에 따라서 cost가 달라질 수 있다고 가정하자

init
4개의 라우터와 4개의 링크가 있고, dest가 다 A이다
B가 보내는 패킷의 트래픽 : 1
C : e
D : 1
지금 아무 패킷이 가고 있지 않은 링크는 cost가 0이다
recompute routing
B->A는 e+1인데, 반대는 0이기 때문에 반대가 더 나을 것이라고 판단한다
C->A로 보낼 때 D 방향이 0이므로 C도 D 방향으로 C->D->A 방향으로 판단한다
recompute...
이런 과정이 계속 반복됨
-> 문제가 된다
모든 라우터들이 최적의 경로만 찾다 보니까 결국 한쪽으로 몰리게 된다
1. 모든 라우터가 LS를 이용하지 않도록 한다 (얼마나 많은 노드들에게 알려야하는가?)
2. traffic에 의존하지 않도록 한다
Bellman-Ford
=> Distance vector algorithm

x를 src, y를 dst라고 보자
distance vector라고 하는 것들이 존재한다.
\(d_{v_1}(y)\) = 3 : \(v_1\) -> y 의 최소 cost가 3
\(d_{v_2}(y)\) = 6
\(d_{v_3}(y)\) = 12
\(d_{v_4}(y)\) = 4
x -> \(v_1\) -> y : 5 + 3 = 8
x -> \(v_2\) -> y : 5 + 6 = 11
x -> \(v_3\) -> y : 7+12 = 19
x -> \(v_4\) -> y : 6 + 4 = 10
이것이 distance vector 알고리즘의 원리이다
- x는 전체 네트워크의 topology와 link cost를 몰라도 됨
- 직접 연결된 라우터로의 cost : C(x, \(v_i\))
- 이웃 라우터들의 최소 cost : \(d_{v_i}(y)\)
만 알면 된다.
Example

각 노드 x, y, z가 테이블을 3개씩 가지고 있다.

이 테이블을 시작 시의 테이블이다
시간에 따라서 테이블이 변화한다 -> 업데이트 되면 변화한다
의미있는 정보들을 다른 노드들에게 알려준다

두번째 업데이트에서 노드 x에서 0 2 3이 되는 것에 대해서 자세히 알아보자
\(D_x(y)\) = min(C(x,y) + \(D_y(y)\), C(x,z) + \(D_z(y)\)) = min(2+0, 7+1) = 2
\(D_x(z)\) = min(C(x,y) + \(D_y(z)\), C(x,z) + \(D_z(z)\)) = min(2 +1, 7+0) = 3
노드 z에서 3 1 0이 되는 것도 확인해보자
\(D_z(x)\) = min(C(z,x) + \(D_x(x)\), C(z,y) + \(D_y(x)\)) = min(7+0, 1+2) = 3
업데이트 이후에는 자신의 정보에 대해서 브로드캐스팅을 한다
단점
Link cost changes


- node detects local link cost change
- updates routing info, recalculates distance vector
- if DV changes, notify neighbors
큰 값에서 작은 값으로 가는 것은 업데이트가 매우 빠르게 된다


작은 것에서 큰 것으로 바뀔 때는 업데이트가 종료될 때까지 시간이 아주 오래 걸린다
y의 테이블에서는 y->z->x의 path가 더 좋다고 생각하게 되고, z는 y로 보내는게 더 효율적이라고 생각하여 이상한 상황에 도달한다
=> poisoned reverse로 해결할 수 있다
수렴 이전의 문제
z, y는 서로 좋다고 생각하는 path가 달라지게 된다.
결국 무한 루프에 돌게 된다
Poisoned reverse
무한루프를 도는 것을 해결할 수 있다
무한 루프를 도는 곳에서 한쪽을 무한대로 설정함으로써 강제로 한쪽으로 보내버리는 것이다
일반적인 네트워크에서는 해결책이 될 수 없다
LS vs DV
message complexity
LS : with n nodes, E links -> O(nE)
DV : exchange between neighbors only - convergence time varies
=> DV가 더 짧다
Speed of convergence
LS : O(n^2) algorithm requires O(nE) msgs
DV : convergence time varies
=> LS가 더 빨리 수렴한다
Robustness
LS가 DV보다 더 Robustness하다
어떤 라우터가 문제가 생겼을 때 LS가 덜 이상한 행동을 하게 된다
Error Propagation
에러가 계속 전파되면서 에러가 계속 커지는 현상
'CS > Computer Network' 카테고리의 다른 글
| [Link Layer] MAC protocols (1) | 2024.12.13 |
|---|---|
| [Link Layer] Error Detection & Correction (0) | 2024.12.12 |
| [Network Layer] IP addressing (1) | 2024.10.18 |
| [Network Layer] Routing (0) | 2024.10.18 |
| [Transport Layer] TCP (1) | 2024.10.17 |