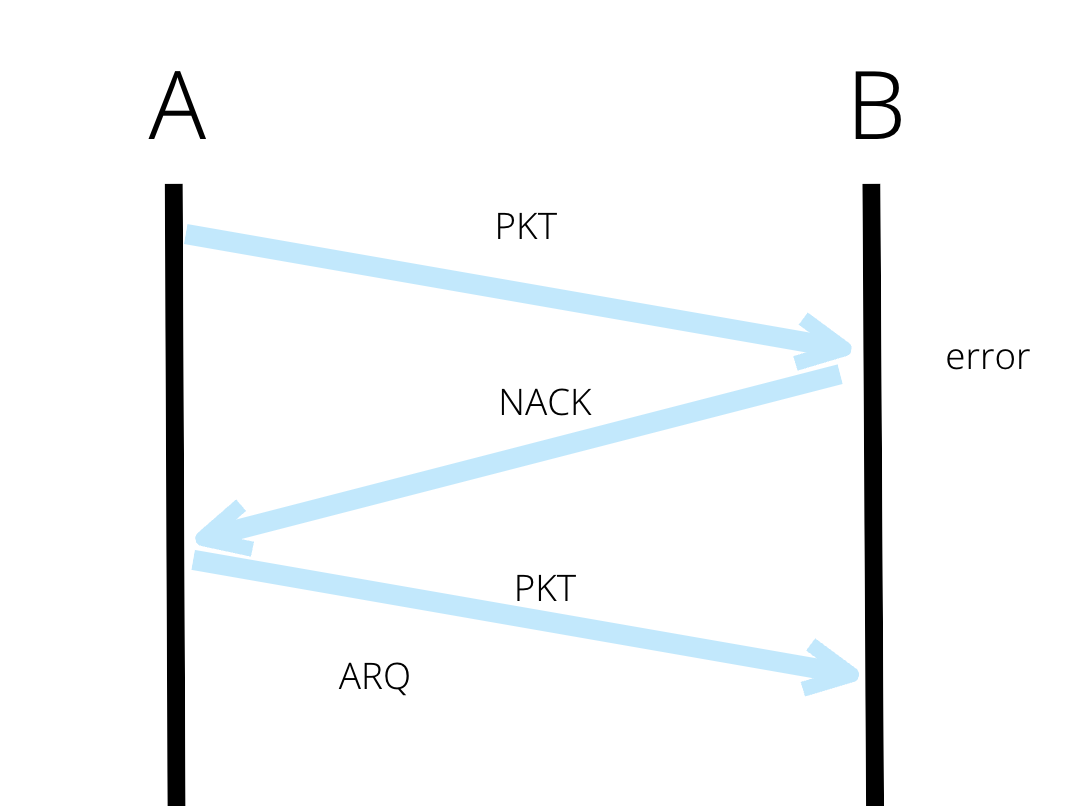
Reliable data Transfer
- flow control : dst에서 데이터를 처리하는 속도보다 src가 더 빨리 보내지 않도록 하는 것
- error control
- error detection : retransmission 요구(ARQ) -> 패킷에서 한 비트만 에러가 발생하더라도 다 버리게 되어있음
- error correction : 문제가 있는 비트를 맞게 바꿔줌 (Forward Error Correction)


feed back <-> feed forward

feed back 시스템은 다시 보낸 시도가 어떠한 시스템에 영향을 미치는데
feed forward는 정방향으로만 흐름이 흐른다. 즉, 다시 되돌아가서 영향을 미치지 않음
ex)
12개의 비트로 이루어진 패킷이 있다고 가정해보자
| 1 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 |
에러가 발생했다고 가정하자
| 1 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 1 |
수신을 받는 입장에서는 해당 부분에서 에러가 발생했는지 알 수 있는 방법이 없음
-> 이를 위해 parity 를 붙인다
| 1 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 1 |
뒤에 파란색 parity 를 붙인 것이다
parity는 data bit에 dependent하게 생성된다
1101이라는 데이터를 보낼 때,
1101을 xor하면 1이 된다 (1xor1 =0, 0 xor 0 = 0, 0 xor 1 = 1) -> 이 뜻은 다 더한 후 mod 2를 해줘도 된다
parity를 1로 설정하면 5개의 bit을 전부 xor 연산 (즉, 더한 후 mod2)하면 0이 된다
그러면 1101이라는 데이터 중 하나가 오류가 생겼을 때, 수신자가 더한 후 mod2 한 값이 0이 되지 않는다.
따라서 무언가 이상하다, error가 있다는 것을 확인할 수 있다
만약 2 비트에 에러가 생겨서 parity 가 맞게 되면, error을 검출할 수 없다
* error correction에서는 더 많은 parity bit가 필요하다
parity bit가 많아지면 데이터의 크기가 줄어들고, 오버헤드가 늘어난다는 단점이 존재한다.
n bit codeword = m data bits + r check bits
code rate = m / n
아까 본 예시에서 보면 12/15 (순수하게 information이 차지하는 비율)
Hamming distance
=> error detection
information bit와 check bit이 명확하게 구별이 되는 것은 아니다
ex)
m = 2, r = 5, n = 7
information bit는 4가지 케이스가 나오게 된다
00 -> 1101011 (꼭 00이 연속되어 있을 필요는 없고 아무데서나 붙을 수 있다)
01 -> 1001110
10 -> ~
11 -> ~
이런 식으로 매핑이 된다
00, 01만 생각해보자
1101011
1001110
두 개를 비교해봤더니 같은 위치에서 다른 비트는 3개이다 -> 이것이 hamming distance이다
hamming distance가 커야지 error을 correction하거나 detection할 수 있는 능력이 커진다
00을 전송했는데, 중간에 error가 발생하여 01을 전송했다고 가정하자
그러면 수신자는 01을 받았다고 생각하여 error을 탐지할 수 없다
왜 error에 취약한 것인가?
2bit의 경우, hamming distance가 1이기 때문에, 한 비트만 달라져도 그것이 받는 입장에서는 옳은 비트라고 생각하게 된다
아까 본 긴 예시로 돌아와 보자
1101011
1001110
해당 부분 중 한 곳이 bit 오류가 나서
1001011이 되었다고 하면
원래 약속된 두 가지의 codeword랑 다르기 때문에 에러가 발생했다는 것을 알 수 있다.
또한, 해당 오류가 난 비트가 hamming distance가 첫번째와는 distance가 1차이, 두번째와는 2차이가 난다.
물론 ARQ를 보내서 다시 보낼 수 있지만 리소스를 줄이기 위해, correction을 진행할 수 있다
1번일 확률이 더 높기 때문에 1번이 전송되었다고 판단할 수 있다.
우리가 지금 총 n 비트를 하나의 codeword라고 부르고 그것들을 모은 것을 code라고 부르는 것이다.
hamming distance of a code : min hamming distance between any codewords
최소 codewords의 해밍 거리가 code의 해밍 거리이다
모든 codeword 마다 다른 해밍 거리를 가지고 있지만 그 중 가장 작은 것을 기준으로 한다는 것이다
왜냐하면 가장 가까운 곳에서 에러가 발생하기 때문이다.
해밍거리가 D일때, error을 detection 할 수 있는 갯수가 D-1 이다.
error을 correction 할 수 있는 갯수는
To detect d errors -> D-1
To correct d errors ->
ex)m = 1, r = 4, n = 5
0 -> 00000
1 -> 11111
hamming distance = 5
11111을 보냈다고 가정하자
error 3 : 00011
error 4 : 00001
error 5 : 00000 -> 오히려 맞다고 판단함
또한, 3,4,5개의 bit의 오류가 발생하는 경우, 00000과 더 가깝기 때문에 correction 할 수 없다.
Parity check code
- Error Correction (X)
- Error detection (O)
이 패킷의 모든 1을 더했을 때 합이 홀수가 되는지 짝수가 되는지 handshacking 단계에서 정해놓으면 된다
00 -> 000
01 -> 011
10 -> 101
11 -> 110
이때 minimum hamming distance = 2 이다
000과 001의 distance가 2이다. 따라서 error detection을 1개 할 수 있다.
01 -> 011 -> 111은 error (D=1) / 101이 되면 no error (D=2)로 인식한다.
또한
00 -> 00000 00000
01 -> 00000 11111
10 -> 11111 00000
11 -> 11111 11111
hamming distance 최소값 = 5
만약 00000 10100이 왔다면, 가장 거리가 적은 code word (2) 인 00000 00000인식하고 00을 전송한다
correction = 5-1/2 = 2bit error correction 가능
detection = 5-1 = 4bit error detection 가능
n 개의 information 중 1개의 error만 correct 할 수 있는 code를 만들고 싶다
m = 2 (2+r) bits 에서 1 bit의 error가 발생하면 알맞은 bit를 알 수 있도록 하고 싶다
만약, 3번 반복하도록 code를 만들면
00 -> 000000
01 -> 010101
10 -> 101010
11 -> 111111
이렇게 되면 hamming distance = 3, 2개를 detection 할 수 있고, 1개는 correction할 수 있다
하지만 이렇게 parity bit이 많아지면 overhead가 커진다
minimum number of check bit을 알아보고자 한다.
2개의 information bits가 있고, n bit짜리 codeword로 매핑이 된다
00 -> 00000으로 매핑이 된다고 생각해보자.
1 bit의 오류가 나는 경우의 수가 총 n개가 존재한다.
만약 01 -> 01000인데, 00000을 보냈는데 01000을 받는다면, 수신자 입장에서는 01로 인식할 것이다.
따라서, 매핑을 할 때 1bit 차이가 나는 것으로 매핑이 되면 안된다 ( hamming distance가 1차이 이상 나야만 한다)
즉, 00000과 hamming distance가 1인 것들은 01000, 10000, 00100, 00010, 00001 과 다른 것을 매핑할 수 없다
따라서 00000과 매핑되더라도 hamming distance가 1인 것들도 강제로 매핑할 수 없다.
(n+1) 개 codeword가 reserved 되는 것이다
m data bits (information bits)
n bits로 구성된 codeword로 구성된 총 개수는
따라서
n = m + r
n + 1 ≤
ex) m = 2 information bit일 때
r = 1 n = m+r= 3 4 ≤ 2
r = 2 n = m+r = 4 5 ≤ 4
r = 3 n = m+r = 5 6 ≤ 8
1 bit error를 고치려면 r =3 의 check bits이 있어야한다.
이에 따른 core rate = 2/5 = 40%이다.
만약 m =4, r =3 하면 code rate 4/7=60%이므로 현재 낭비되고 있는 것을 볼 수 있다. (정확히 equal하는 것)
=> (7,4) 를 hamming code라고 한다. (정확히 같은 것)
* 2bit를 고치고 싶다면 (n+1) 대신 nC2+1을 사용할 수 있다
Hamming code
Each check bit forces the parity of same collection off bits including itself
ex)
data = 1011 (m = 4)
n = 7, r = 3
_ _ 1 _ 0 1 1
이렇게 되어있다고 하자. 빈 칸은 parity이다
여기에 어떤 parity를 넣어야할까?
k = 1 :
k = 2 :
k = 4 :
* k = 3 =
k = 5 =
k = 6 =
k = 7 =
로 되어있다.
k = 1을 보면
k = 2를 보면
k = 4를 보면
따라서 저 빈칸에 들어가는 parity 는 0 1 0이 된다.
이러한 방식이 hamming code의 encoder 부분이다
encoding : information bit를 codeword로 하는 것
decoding : encoding된 information을 다시 원래 information bit로 복원하는 것
해당 예시로 다시 돌아가보자.
따라서 해당 예시에서 encoding된 bit는 0 1 1 0 0 1 1 이다.
이를 전송했는데 0 1 1 0 0 1 1 -> 0 1 1 0 1 1 1 로 5 bit에서 오류가 났다고 가정하자\
parity
k = 1 : 0 / k = 3,5,7 -> 오류를 기준으로 1 1 1 -> 1 => error
k = 2 : 1 / k = 3,6,7 -> 1 1 1 -> 1
k = 4 : 0 / k = 5,6,7 -> 1 1 1 -> 1 => error
error bit = (k = 1) + (k = 4) = 5
따라서 5bit에서 에러가 발생했다는 것을 알 수 있다
ex)
m = 4
0 0 0 0 -> 0 0 0 0 0 0 0
0 0 0 1 -> 0 1 0 0 1 0 1
0 0 1 0 -> 0 0 0 1 0 1 0
... 총 16개가 존재한다
수신자가 0 0 1 0 0 0 1을 받았다고 할 때, hamming distance가 가장 짧은 것을 선택할 수 있다
하지만, 이런 경우 모든 code word와 비교하면 되는데 연산량이 매우 늘어난다
그래서 hamming code처럼 비교해서 하면 효율적으로 비교할 수 있다
1 dimension
00 -> 000
01 -> 011
10 -> 101
11 -> 110
일 때 hamming distance = 2이다
따라서 1bit error detect, 0bit error correction할 수 있다
2 dimension
ex) 0100
2차원으로 배열 하고 parity를 5bit를 붙이는데,
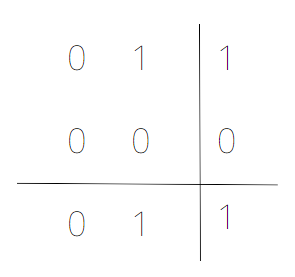
해당 그림처럼 행 열 그리고 그 계산한 결과로 parity 를 붙인다
만약 여기서 에러가 발생하게 된다면 각 행과 열에서 문제가 생기기 때문에 이를 통해서 어디서 error가 생겼는지 알 수 있다
CRC code
Error을 detect하기 위해서 사용하는 code
- source coding : 압축 ( = compression)
- channel coding(FEC) : error 보정 (error로부터 protection)
m개 bits + r개 bits (CRC)
위에서 본 parity의 경우, 2개의 error가 생기게 되면 error가 나지 않았다고 판단한다.
CRC의 경우
1) error의 개수가 홀수개 : 무조건 detect
2) #burst error ≤ r : detect 가능함 -> 짝수가 detect 가능한 조건
*butst : 연속된
'CS > Computer Network' 카테고리의 다른 글
| [Physical Layer] 통신 시스템 & SNR (0) | 2024.12.14 |
|---|---|
| [Link Layer] MAC protocols (1) | 2024.12.13 |
| [Network Layer] Routing Algorithm (0) | 2024.12.12 |
| [Network Layer] IP addressing (1) | 2024.10.18 |
| [Network Layer] Routing (0) | 2024.10.18 |