통신 시스템

Bit Source
모든 신호는 bit stream으로 표현한다.
4 x 4로 표현된 이미지가 있다고 생각해보자
16 pixels x 8 = 128 bits가 된다
Symbol mappping
bitsteam을 symbol로 매핑한다.

j는 복소수이고
s1 = 1+j (00)
s2 = 1-j (01)
s3 = -1-j (10)
s4 = 1-j(11)
과 같이, 위상 변화를 90씩 주어 4개 종류의 디지털 심볼로 전송하는 4진 PSK 방식이다
그에 따라 128bit는 64 symbol이 된다
noise
채널에서 신호 전송 중 외부 요인에 의해 신호에 추가되는 불필요한 전기신호
송신단에서 수신단으로 전달할 때
- 신호 감세
- fading
- noise
- 효과가 발생함
- 전자 회로에서 random motion(noise)가 발생한다. (-275도에서는 노이즈가 발생하지 않는다)
ex1) noise = 0.2-j0.1이라면,
수신 symbol r = s + n
= 1 + j + 0.2 - j0.1 = 1.2 + j0.9이다
ex2) s= 1+j / n = -1.2-j0.2
r = s + n = -0.2 +j 0.8
=> s' = -1+j
00 인데 01로 판단하게 된다 -> 1 bit error
Decision
s = 1 + j를 추측하는 것 처럼 한다
s' = min || r - Sj || = 1 + j
수신된 신호 r을 가장 가까운 심볼로 판단하여, 거리가 가장 짧은 심볼을 선택한다
Demapper
Decision 한 bit로 전환한다.
ex1의 경우 송신한 bit00, 수신한 bit00이다
ex1과 2에 대한 표현이다


QUIZ
Quiz 1
두 개의 4QAM이 존재할 때,더 좋은 것은 무엇인가?


정답은 왼쪽이다
gray mapping으로 에러날 때 한 bit만 달라지기 때문에 2보다 더 좋다.
즉, 바로 이웃한 symbol끼리 1 bit 차이만 난다.
ex) 송신 bit 00 + n -> 수신 bit가 왼쪽의 경우 01 (1bit error)이지만, 오른쪽의 경우 11(2 bit error)이다.
여기서 의문이 드는 점
noise가 커서 송신 비트가 00일 때 왼쪽이 11, 오른쪽이 10이 되는 상황에는 오른쪽이 좋은 것 아닌가? 아니다.
왜냐하면 n = a+jb일때, n이 작은 값일 확률이 가우시안 분포(정규 분포)로 되어있기 때문에
noise의 값이 1사분면에서 3사분면으로 갈 확률 < 1사분면에서 2사분면으로 갈 확률이 된다.
Quiz2
16QAM(4 x 4), gray mapping 일 경우, 1 +j에 들어가는 값은 무엇인가?
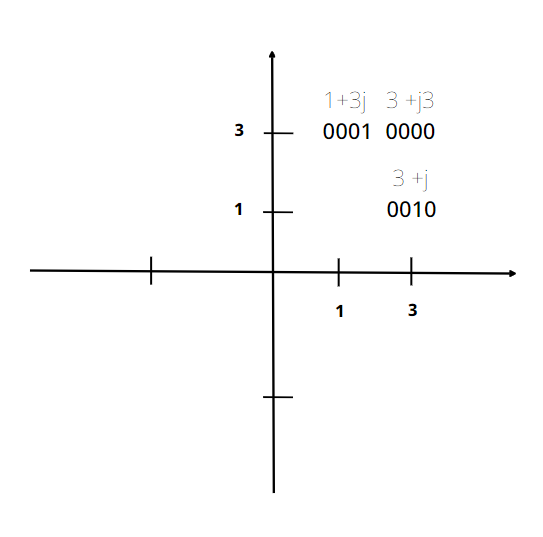
답은 0011dlek.
1symbol 은 4 bits의 정보가 되고, 0000, 0001, 0011.. 등이 symbol에 매핑이 된다.
Bit Error Rate (BER)
BER = error 발생 bit / 전체 bit
ex)
송신단 ) 0 1 0 1 1 0 0 1 0 1
수신단 ) 0 1 0 1 0 0 1 1 0 1
노이즈에 의해 빨간 부분에 error가 발생한다.
이때 BER = error 발생 bit / 전체 bit = 2/ 10 = 0.2 이다
SNR(Signal-to-Noise Ratio)
SNR = Signal power / Noise power
SNR이 증가시 BER이 감소한다.
power (전자 회로)
P = VI = \(I^2R\) = \(\frac{V^2}{R}\)
R = 1Ω이라고 가정하면, P = \(I^2\) or \(V^2\)
따라서 P = \(S^2\)이다
현재 s는 랜덤한 값이다.
따라서 \(|s|^2\)도 랜덤한 값이므로 \(E(|s|^2)\) = 예측값, 평균값을 사용한다.
그러면, 노이즈는 어떠한가?
\(E(|s|^2)\) 수신단의 회로에서 어절 수 없이 생기는 값으로 노이즈의 평균이다.
이는, n ~ cN(0, \(\sigma^2\))이다.
c : 복소수 가우시안이며, 분산은 온도와 관련이 있어, 온도가 높을수록 분산이 커진다.
현재 랜덤 변수 x라고 가정할 때, var(x) = E((x-E(x))\(^2\))이다.
현재, 평균이 0이므로, E(x) = 0 => \(E(x^2)\)이 된다.
따라서 \(E(|n|^2)\) = \(\sigma^2\)이 된다.
*n = a +jb 에서, n이 정규분포이면 a와 b도 정규분포이다
ex) signal에 18 4개, 10 8개, 2 4개가 있다고 가정하자
E(|s|^2) = 18 * 4/16 + 10 * 8/16 + 2 * 4/16 = 10이다
따라서 SNR은 \(\frac{10}{\sigma^2}\)이다.
*magnitude(크기) 계산하기
|s| 같은 것들은 크기를 의미한다.
ex) s= 3 -j => |s| = \(\sqrt{3^2 + (-1)^2} = \sqrt{10}\) => \(|s|^2\) = 10
∴ SNR = \(\frac{|s|^2}{|n|^2}\) => \(\frac{|s|^2}{E(n^2)}\) = \(\frac{|s|^2}{\sigma^2}\)
QUIZ
Quiz 1
4QAM일때 SNR은?
\(S_1 = 1 + j\)
\(|S_1| = \sqrt{1^2 + 1^2} = \sqrt{2}\)
\(|S_1|^2 = 2\)
나머지에 대해서도 계산하면 전부 2이다.
따라서 signal average power = 2 이므로
∴ SNR = \(\frac{2}{\sigma^2}\)이다.
QUIZ2
16QAM일 때 SNR은?
\(S_1 = 3 + j3\), \(|S_1|^2 = 18\)
\(S_2 = 3 + j\), \(|S_2|^2 = 10\)
\(S_3 = 1 +j\), \(|S_3|^2 = 2\)
\(S_4 = 1 + j3\), \(|S_4|^2 = 10\)
이 경우 signal average power 는 1/4 (18 + 10 + 2 + 10) = 10
∴ SNR = \(\frac{10}{\sigma^2}\)
Quiz 3
1) QPSK이고, n의 \(\sigma^2\) = 0.02 => SNR? 100
2) 16QAM이고, n의 \(\sigma^2\) = 0.1 => SNR? 100
풀이 )
1) QPSK의 \(E(|s|^2\) = 2이다. (1+j, 1-j, -1+j, -1-j)
SNR = \(\frac{2}{0.02} = 100\)
2) 16QAM의 \(E|s|^2\) = 10이다.
SNR = \(\frac{10}{0.1} = 100\)
BER & SNR
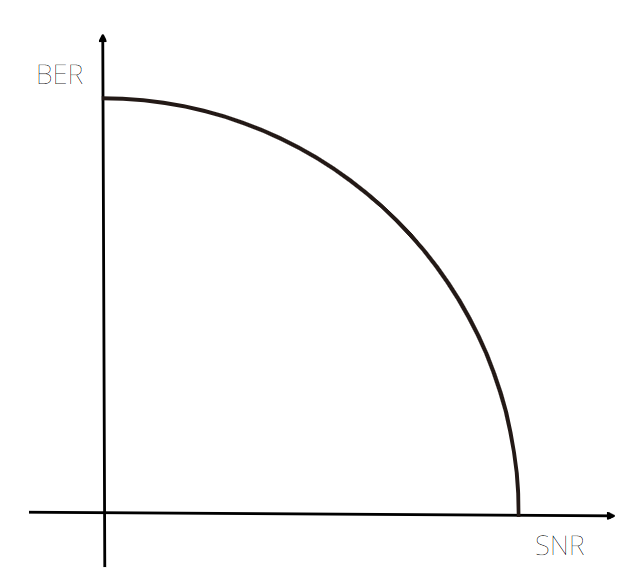
BER과 SNR의 관계를 살펴보면, linear scale일때는 아래로 볼록(convex)상태가 된다.
linear scale의 경우, 폭이 같지 않기 때문에 보기가 아렵기 때문에 log scale인 dB(데시벨)로 변환해서 보겠다.
여기서 BER의 의미를 다시 생각하자면, 0.01은 100비트 보내면 1비트 error가 날 확률이다
log scale로 변환하면 위로 볼록(concave)한 함수가 된다.
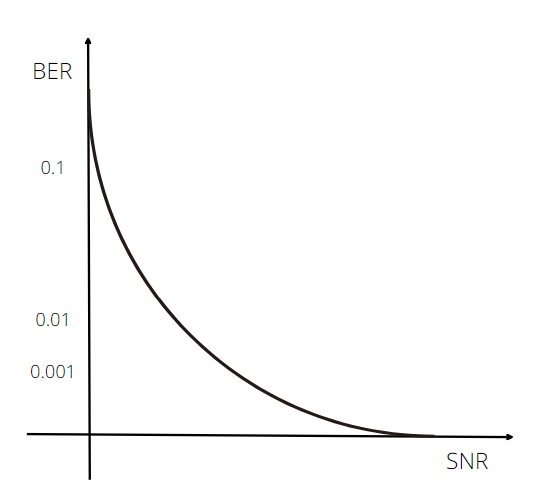
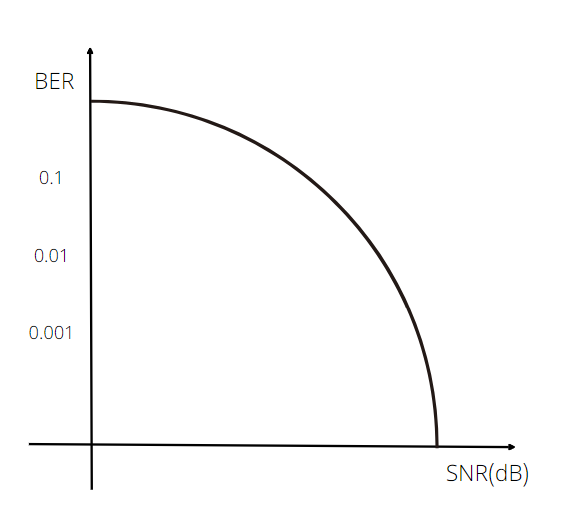
dB : 10log(SNR)이다
따라서, 오른쪽 그림을 기준으로 생각하여 SNR이 클수록 BER이 작아진다는 것을 알 수 있다.
S -> SNR
현재, 4QAM일때 1+j, 1-j, -1+j, -1-j라고 가정하여 계산했을 때, \(E(|s|^2\) = 2가 된다.
만약 1+j가 아니라 0.2+j0.2라고 생각하면 \(E(|s|^2)\) = 0.08이 된다.
즉, SNR이 \(\frac{2}{\sigma^2}\)과, \(\frac{0.08}{\sigma^2}\)이 된다.
s가 클 때, SNR도 증가한다.
이 경우 s가 5배 차이나며, SNR의 경우 25배차이가 난다 -> power가 1/25배 된다.
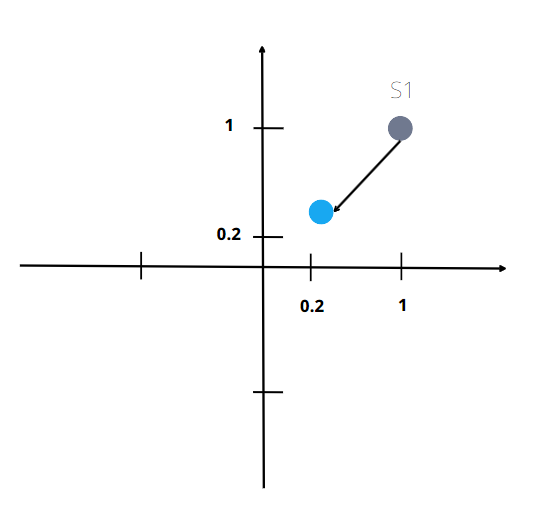
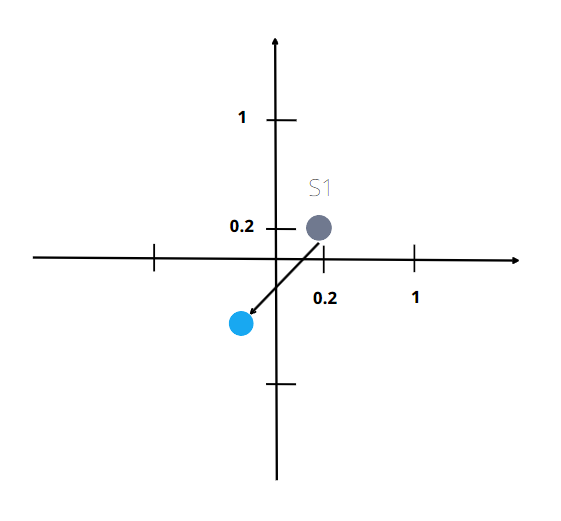
그림에서 처럼, 같은 노이즈가 적용되더라도 s가 작은 경우 error가 발생한다.
QPSK vs 16QAM
| QPSK | 16QAM | |
| power (avg power s) | 1 (s) | 1 (10) |
| BER | good | bad |
| data rate | 낮음 | 높음 |
| required SNR (BER = small) | 낮음 | 높음 |
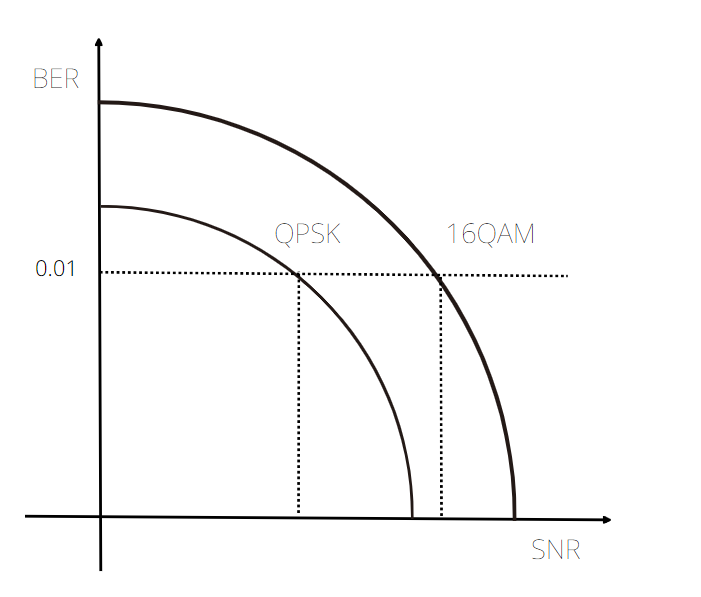
16 QAM이 좋지 않은 것은 맞지만, data rate는 높다.
LDPC(저밀도 패리티 체크)를 이용한다.
Error rate : small하기 원함
avg SNR : QPSK = 17dB / 16QAM 21dB와 같은 상황이 발생한다.
avg SNR이 높아질수록 data rate가 늘어난다
즉, 16AQM의 경우 한 심볼에 4bits를 전송한다.
=> noise가 더해졌기 때문에 AWGN(Additive White Gaussian Noise)라고 부른다.
'CS > Computer Network' 카테고리의 다른 글
| [Physical Layer] Wireless Channel (0) | 2024.12.15 |
|---|---|
| [Link Layer] MAC protocols (1) | 2024.12.13 |
| [Link Layer] Error Detection & Correction (0) | 2024.12.12 |
| [Network Layer] Routing Algorithm (0) | 2024.12.12 |
| [Network Layer] IP addressing (1) | 2024.10.18 |