BST : 최악의 경우는 여전히 좋지 않음 -> AVL Tree로 이를 해결하고자 함

같은 데이터를 가지고 있어도 다른 모양의 트리가 나올 수 있음
오른쪽 경우가 생기는 것을 막아보자
AVL Tree Idea
Root가 어떤 수인지에 따라서, 왼쪽과 오른쪽의 균형이 맞지 않을 수 있음
양쪽의 노드의 개수가 비슷한 것을 선호 : 균형잡힌 트리
→ < 보정 > : 균형 잡힌 트리를 만들기 위해 root의 숫자를 바꿔주고, 트리의 모양을 바꿔줌
Root 뿐만 아니라 서브 트리의 root에서도 보정이 일어날 수 있음
AVL Tree Definition
기본 BST 정의에 추가되는 것
- Each Node has Two Labels : L & R - 각각의 서브트리의 높이
- Condition : |L - R| < 2 즉, L,R이 높이 차이가 0, -1, 1이여야함
→ 모든 노드에서 양쪽 서브트리의 노드 개수가 똑같아 지기 위해서 전체 노드 개수가 \(2^k-1\)개여야만 함
insert / delete가 일어나는 상황에서도 항상 조건을 유지해야함
Height Bound
N개의 노드가 있다면, Height는 O(log N)
→ Search가 O(log N)이 걸린다
< 왜 노드의 개수에 비해 height는 작을까? idea>
모든 서브트리에서 AVL 트리의 정의를 만족해야한다.
만약 한쪽으로 쭉 진행된 트리가 있다면, 마찬가지로 조건을 맞추기 위해 반대쪽에도 비슷한 개수의 노드가 있어야한다
이 조건이 모든 노드를 기준으로 한 서브트리에서 만족해야하므로,
처음에서 높이는 그대로지만, 조건에 맞춰 노드를 늘리다보면, 노드의 개수에 비해 height는 매우 작음을 확인할 수 있다.
즉, 높이에 비해 노드 개수가 많다
Definition
Down Sequence Definition
- String of L & R ex)LRLLRLRLRLRL
- Represents Movment from root : 루트에서부터 따라 내려가는 방향을 표시한 것
- down sequence는 언젠가는 가지 못하는 경우가 생긴다 - 자식이 없는 경우
제일 마지막에 가지 못하는 Down Sequence를 Terminated Down Sequence 라고 하자
Proof : 노드의 개수에 비해 높이가 작다 == 높이에 비해 노드 개수가 많다
루트에서 가장 멀리 갈 수 있는 노드 (leaf) = 가장 먼 terminated down sequence
루트에서 가장 가까이 끝나는 노드 = 가장 가까운 terminated down sequence
* 루트에서 가장 긴 sequence의 레이블은 k, k-1, k-2 ... 0으로 진행됨 (1개씩 줄어듦)
* 루트에서 가장 짧은 sequence의 레이블은 k-1, k -3 ... 0으로 진행됨 (2개씩 줄어듦) + 맨 위에 레이블은 최대 1차이
루트에서 가장 가까이 끝나는 노드까지는 노드가 가득 차 있음 \(2^n\)개→ 균형잡힌 트리이기 때문임
주장을 증명하려면 : 가장 멀리갈 수 있는 노드와 가장 가까이 끝나는 노드와의 거리가 비슷하는 것을 보여야함
Count of nodes
If maximum label on Root is K 만약, 루트 라벨의 최대값이 K라면
Then the height of the Tree is K+1 트리의 높이는 K+1
Then the shortest Terminated down sequence is at least K/2 가장 짧은 terminated down sequence는 K/2
따라서 트리에는 shortest terminated down sequence까지 노드가 다 차있기 때문에 최소 \(2^{K/2}\)개의 노드 존재
노드의 개수 : \(2^{K/2} <= N <= 2^K\)
K/2 <= logN 이므로, K = O(log N)
트리의 높이가 logN이다
Q. How to keep the condition after an insert and delete
A. 특정 노드를 보정하여 루트로 만든다
Insert
- Do the normal insert -> leaf에 하는 것 그대로
- come back up the tree and recompute Label 위로 올라가 리턴하면서 라벨을 다시 설정 (최대 1증가)
- For the first Node to break the condition, perform ROTATION 조건이 깨지는 노드에서 보정

조건이 깨지기 위해서는 K쪽에서 insert가 일어나야함
* 만약 K-1에서 insert가 일어난다면 K가 되기 때문에 조건이 깨지지 않음
새로 추가된 노드는 조건이 깨진 노드에서 최소 두 노드 아래에 있어야함
→ 만약, 바로 아래에 있는 노드에 추가된것이라면 0 -> 1이 된 것이고, 그 전에 조건을 유지중이였으므로 2 이상 차이가 날 수 없음
즉 두 레벨을 더 내려가서 생각해야함
따라서 발생할 수 있는 경우의 수는 LL LR RL RR 총 4가지가 존재
(그림에 따르면, k-1 = 0일때 새로 생긴 노드는 D 혹은 E일 수도 있음, 그 아래 서브트리를 통틀어서 생각해도 됨)
Q. B가 왜 K-1 K-1로 같은가?
A. 만약 B의 서브트리 중 하나에 노드가 하나 추가된다면, 한 쪽에 +1이 될 것이다. 따라서 무조건 1의 차이가 생기게 되는데, 만약 B의 라벨이 k-2와 k-1이였다면, k-1에 노드가 하나 추가될 때, 균형이 깨지므로 A가 첫번째로 조건이 깨진 트리라는 전제가 깨지게 된다
*Case는 *첫번째로 condition이 깨지는 경우를 의미!
Case LL
D, 혹은 D의 서브트리에 insert
- B를 부모노드, A는 B의 자식노드가 됨
- A의 부모노드가 있었다면, A의 부모노드는 B를 가리킴
- E는 A의 왼쪽 노드가 됨
결과
- B의 라벨은 K, K (왼쪽에 insert가 되고, A가 B의 자식노드가 되면서 하나가 늘어남)
- A의 라벨은 K-1, K-1 (왼쪽 자식노드였던 B가 올라가면서 왼쪽 노드가 하나 줄어듦)
Case LR
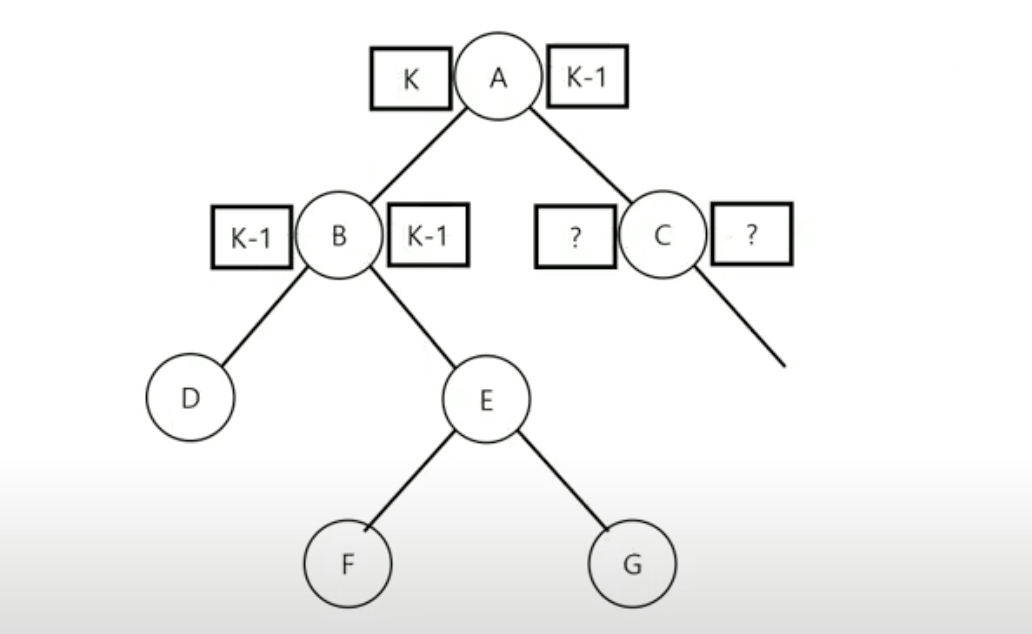
E, 혹은 E의 서브트리에 insert
- E가 부모노드가 됨
- B는 E의 왼쪽, A는 E의 오른쪽 노드가 됨
- F가 있다면, B의 오른쪽 노드, G가 있다면 A의 왼쪽 노드
결과
- B의 오른쪽 노드는 E가 올라가면서 K-2가 됨 - 만약 F에 insert된거라면, K-1이 됨
- A의 왼쪽 노드는 E가 올라가면서 K-2가 됨 - 만약 G에 insert된거라면, K-1이 됨
- E는 양쪽 모두 K 라벨을 가짐 (B는 왼쪽, A는 오른쪽에 무조건 K-1개의 노드를 가지기 때문)
Case RL
RL에 즉, C아래에 노드 T가 추가된다고 가정
- RL에 있는 노드가 부모노드가 됨 (T가 부모 노드가 됨)
- T의 왼쪽 노드는 A, T의 오른쪽 노드는 C
- 나머지는 LR과 같은 방식으로 자식 노드로 들어가게 됨 (A의 오른쪽, C의 왼쪽)
Case RR
RR에 즉, C 오른쪽에 노드 S가 추가된다고 가정
- 노드 C가 부모 노드가 됨
- 노드 C를 기준으로 노드 A는 왼쪽, 노드 S는 오른쪽 노드가 됨
'CS > Data Structure' 카테고리의 다른 글
| Priority Queue (1) | 2024.06.12 |
|---|---|
| AVL Tree Variation(2-3 Tree, 2-3-4 Tree, Red-Black Tree, skip list) (2) | 2024.06.12 |
| Binary Search Tree (0) | 2024.04.24 |
| Equivalence class 코딩 (0) | 2024.04.23 |
| Linked List (2) | 2024.04.21 |