Subgraphs
그래프의 일부
Defintion
Let G = (V,E) and H = (W,F) be graphs. H is said to be a subgraph of G, if \(W\subseteq V\) and \(F\subseteq E\)
G와 H가 모두 그래프이고, W가 V의 부분집합, F가 E의 부분 집합일 때 subgraph라고 한다
Q.How many \(Q_2\) subgraphs does \(Q_3\) have?
A. 같다의 약한 개념에서는 6, 강한 개념에서는 1개이다
노드에 번호를 부여하였을 때, 노드의 번호가 다르다면, 다른 그래프이기 때문에 \(Q_2\)에 1,2,3,4라는 노드 번호와 일치해야한다.
Unions

강하게 같다 라는 개념을 사용하여 Q.How many \(Q_2\) subgraphs does \(Q_3\) have? 문제를 생각해보자
모두 다른 6개의 \(Q_2\)그래프로 \(Q_3\)그래프를 만드는 것이다
Definition
Let \(G_1 = (V_1, E_1)\) and \(G_2 = (V_2, E_2)\) be two simple graph. The union of \(G_1, G_2\) is formed by taking the union of the vertices and edges
\(G_1\bigcup G_2 = (V_1 \bigcup V_2, E_1 \bigcup E_2)\)
Adjacency Matrix

adjacency여부를 행렬로 표현한 것
directed graph : i→ j인 edge가 존재하면 1, 없으면 0으로 표시하는 행렬
directed multigraph : 행렬에 edge의 개수를 나타냄
undirect graph : 양방향을 가리키는 그래프가 있다고 생각하여 모든 edge를 복사하여 인접 행렬에 나타낸다 (즉 대각을 축으로 대칭이며, 대각선의 영역은 self loop가 있다면 2이다)
Graph Isomorphism
그래프가 완전히 같다는 것이 아니라 그래프의 모양이 같다
노드 번호를 붙이면 다른 그래프지만, 번호를 잘 붙이면 같은 그래프를 만들 수 있다
Graph Isomorphsim undirected graphs
Definition
Suppose \(G_1 = (V_1, E_1)\) and \(G_2 = (V_2, E_2)\) are pseudographs. Let f:\(V_1\)→\(V_2\) be a function s.t.
1) f is bijective 일대일 대응
2) for all vertices u, v in \(V_1\) the number of edges between u and v in \(G_1\)is the same as the number of edges between f(u) and f(v) in \(G_2\)
\(V_1\)에 있는 u,v에 대해 u에서 v로 연결하는 edge의 개수가 \(G_1\)에서 연결하는 f(u), f(v)를 연결하는 edge의 개수와 같아야한다
즉, 함수 f로 매핑했을 때 같은 그래프가 되어야한다
Graph Isomorphsim digraphs
Definition
Suppose \(G_1 = (V_1, E_1)\) and \(G_2 = (V_2, E_2)\) are directed multigraphs. Let f:\(V_1\)→\(V_2\) be a function s.t.
1) f is bijective 일대일 대응
2) for all vertices u, v in \(V_1\) the number of edges from u to v in \(G_1\)is the same as the number of edges between f(u) and f(v) in \(G_2\)
\(V_1\)에 있는 u,v에 대해 u에서 v로 가는 edge의 개수가 \(G_1\)에서 연결하는 f(u), f(v)를 연결하는 edge의 개수와 같아야한다
*2번 조건에서 between 인지, from-to인지에 따라 달라짐 - 즉 순서의 유무
Properties of Isomorphims
- number of vertices and edges
- degrees at corresponding vertices
- types of possible subgraphs
이러한 조건이 지켜지지 않는다면 isomorphism하지 않다고 볼 수 있음
Path
A path in a graph is a continuous way of getting from one vertex to another by using a sequence of edges
Definition
A path of length n in an undirected grah is a sequence of n edges \(e_1\), \(e_2\), \(e_3\)... and it has node \(V_1\), \(V_2\),\(V_3\)... such that each consecutive pair \(e_i, e_{i+1}\)share a common vertex
edge사이에 노드가 존재하며, edge의 연속되는 순서쌍에서 사이에 어떠한 노드가 존재해야한다.
Definition - simple path
contiains no duplicate edges
edge가 반복되지 않는 path
Definition - Directed graphs
target of \(e_i\) is the source \(e_{i+1}\) for each i
Connectivity
Definition
Let G be a pseudograph. Let u and v be vertices. u and v are connected to each other if there is a path in G which starts at u and ends at v.
G is said to be connected if all vertices are connected to each other
자신과 자신도 connected로 볼 수 있음
Connected components
Definition
A connected component in a graph G is a set of vertices such that all vertices in the set are connected to each other and every possible connected vertex is included
분리되는 그래프들이라고 생각할 수 있음
N-connectivity
Not all connected graphs are creaded equal 연결된 그래프이지만, 연결의 능력이 다르다 - 일부가 고장나도 돌아가느냐?
cut vertex : 끊어지면, 전체적인 연결이 끊기게 되는 노드
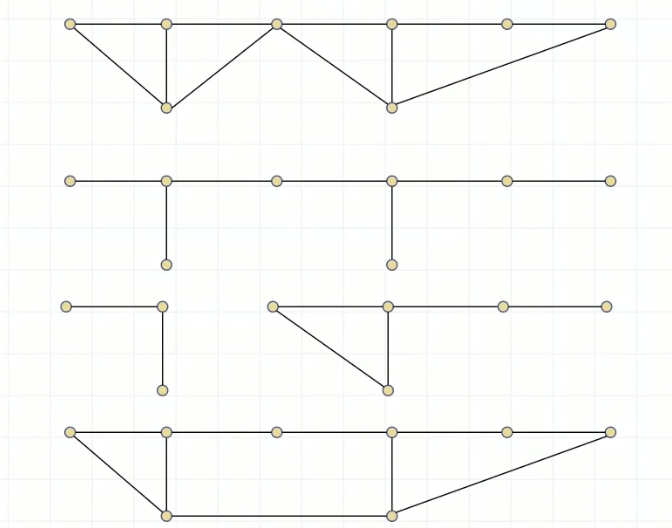
4번은 cut vertex가 없다 - 두 개의 노드가 끊어져야만 연결이 끊긴다 (2-connected
Definition 2-connected / cut vertex
A connected simple graph with 3 or more vertices is 2-connected if it remains connected when any vertex is removed. when the graph is not 2-connected, we call the disconnecting vertex a cut vertex
두개의 노드를 지워서 그래프가 끊어지는 것은 2-connected / 하나만 끊어도 되는 노드를 cut vertex라고 한다
Q. simple graph의 개수 제한은 왜 있는걸까?
A. 노드 2개로만 이루어진 그래프를 제외하기 위해서
Connectivity in Directed Graphs
방향을 역전할 수 없기 때문에 단순히 연결되어있는 undirected graph와 같게 생각할 수 없음
1) Weakly connected : can get from a to b in underlying undirected graph
2) Semi-connected : can get from a to b or from b to a in digraph
3) Strongly connected : can get from a to b and from b to a in the digraph
graph 전체에서 어떻게 connected 되어있는지 정의할 수 있음
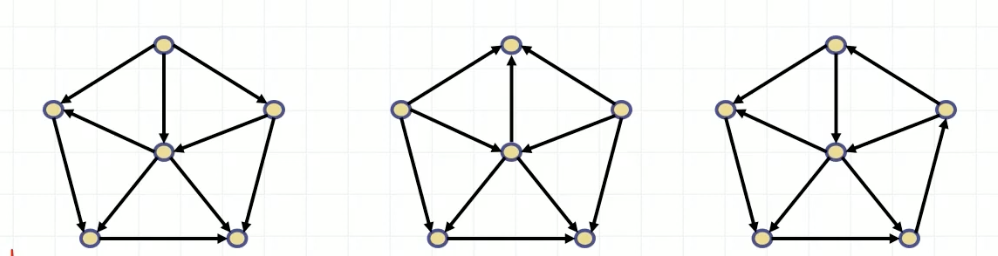
모든 두가지 노드에 대해서 어떤 connect가 가능한지 다 찾으면 됨
만약, semi나 strong은 반례를 하나를 가지면 안된다
weakly connected :전부 가능
semi-connected : 가능 / 불가능 / 가능
strongly connected : 불가능 / 불가능 / 가능
*strongly connected는 사이클에 들어 있어야함 (세번째 그림의 경우, 전체적으로 오각형 큰 사이클이 존재함)
행렬과 Path
행렬을 보고 path의 개수가 몇 개인지 확인할 수 있음
ex) 구글의 page rank
- 길이 별로 개수를 셈 ex) 길이 1, 길이 2, 길이 3 ...
- 길이 k번째에서 x에서 y로 가는 path의 개수가 몇 개 있는지 표시하는 행렬을 만듦
- 길이 k번째 행렬과 기존의 인접 행렬 두개의 행렬을 곱함 → 다음으로 갈 수 있는 행렬의 path의 개수를 구함 (k+1)
'CS > Data Structure' 카테고리의 다른 글
| Quick Sort (0) | 2024.09.10 |
|---|---|
| HALTING Problem (0) | 2024.09.03 |
| Graph (Undirected, Digraphs, Graph Patterns) (2) | 2024.06.18 |
| Union Find (10) | 2024.06.13 |
| Tree Traversal & Parsing (0) | 2024.06.13 |