Graph basics and definitions
- Vertices / nodes : 노드, 점
- edges : 선
- adjacency / incidence : 인접 - 두개의 뜻이 어떻게 다를까?
- Degree, in-degree, out-degree : 차수
- Subgraphs, unions, isomorphism
- Adjacency matrics (인접 행렬)
Graph의 종류
- Trees
- Undirected graphs - simple graphs, Multigraphs, Pseudographs
- Digraphs, Directed multigraph
- Bipartite
- Complete graphs, cycles, wheels, cubes, complete bipartite
Intuitive Notion
- 정의
A graph is a bunch of vertices (or nodes) represented by circles which are connected by edges, represented by line segments
edge로 이루어져있는 노드들 - 수학적 정의
Mathmatically, graphs are binary-relations on their vertex set
노드들의 집학에 대한 binary relation
Undirected graph
Simple graphs
ex) local computer network - bidirectional(양방향이지만, 방향이 없음) / no loops(스스로 연결되지 않음) / unique connections(중복되어 연결될 필요가 없음)
*endpoints : edge가 연결하는 두 노드
- Each edge can be viewed as the set of its two endpoints
edge는 두 개의 endpoints를 원소로 가진 집합으로 생각할 수 있음
Definition
A simple graph G = (V,E) consists of a non-empty, finite set V of vertices and a set E of edges where each edge is a subset of V with cardinality 2 (unordered pair)
simple graph는 V(node set)과 E(edge set)의 순서쌍으로 node set V는 공집합이 아니고 유한하며, edge set E는 사이즈가 2인 순서 없는 V의 부분집합(V의 원소들로 만들어짐)이다.
Q. For a set V with n elements, how many possible edges there? V가 n개면 서로 다른 edge의 개수는?
A. \(_nC_2=\frac{n(n+1)}{2}\) n개에서 2개를 뽑는 경우의 수와 같음
Q. How many possible graphs are there for the same set of vertices V? V가 n개면 만들 수 있는 그래프의 개수는?
A. 그래프가 같다는 것은 \(G_1 = (V_1, E_1)\)와 \(G_2 = (V_2, E_2)\)이 있을 때, \(G_1 = G_2 \Leftrightarrow\) \(E_1 = E_2\) & \(V_1 = V_2\)
모든 edge의 경우의 수에서, edge의 존재여부에 따라 다른 graph를 만들 수 있으므로 \(2^{\frac{n(n+1)}{2}}\)
Multigraphs
ex) computers are connected via internet - 여러개의 길이 있을 수 있음
* function : Labeling the edges (edge에 이름을 붙이고, 그 edge가 어떤 노드와 연결되어 있는지 function으로 정의함)
Definition
A multigraph G = (V,E,f) consists of non-empty set V of vertices, a set E of edges and a function f with domain E and codomain the set of unordered pairs in V
multigraph는 공집합이 아닌 유한한 노드의 집합 V와 edge의 집합 E, 그리고 정의역을 E, 치역을 순서없는 V의 쌍으로 정의하는 함수 f로 이루어진다
Pseudographs
graph that allow the self-loop
Definition
A pseudograph G=(V,E,f) consists of a non-empty set B of vertices, a set E of edges and a function f with domain E and codomain the set of unordered pairs and singletones in V
multigraph는 공집합이 아닌 유한한 노드의 집합 V와 edge의 집합 E, 그리고 정의역을 E, 치역을 순서없는 V의 쌍 혹은 하나(self-loop가 허용되기 때문)로 정의하는 함수 f로 이루어진다.
용어
adjacent (인접) : if they are the endpoints of the same edge 직관적으로 edge를 타고 한번에 갈 수 있으면 "인접"하다
incident (인접) : with an edge if it is the endpoint of the edge
*adjacent vs incident : adjacent는 노드와 노드의 관계, incident는 노드와 edge의 관계
Digraphs
*undirected graph의 경우, ordered 되어있지만 대칭성이 존재하여 (a,b)와 (b,a)가 동치관계이므로 방향이 없는 것과 같음
directed graph에서는 처음부터 self loop를 허용할 수 있음 (a,a)의 관계가 자연스럽기 때문
- Each edge is directed so an ordered pair(tuple) rather than unordered pair
edge는 순서쌍으로 이루어짐
Definition
A directed graph(or digraph) G = (V, E) consists of a non-empty and finite set V of vertices and a set E of edges with \(E\subseteq V\times V\)
방향이 있는 그래프는 공집합이 아니고 유한한 집합 V와 VxV집합의 공집합인 edge집합 E로 이루어짐
The edge (a,b) is also denoted by a → b and a is called source of edge, while b is called target of the edge
(a,b)에서 a에서 b로 가는 방향이며, a는 source b는 target이라 한다
Q. For a set V with n elements, how many possible digraphs are there?n개의 V집합이 있다면, 몇개의 방향 그래프가 생성되는가?
A. 가능한 edge의 개수는 \(n \times n\) 이며, edge의 존재 유무에 따라 다른 그래프가 되기 때문에 총 \(2^{n\times n}\)개
Directed Multigraphs
same as undirected multi graphs but has direction
용어
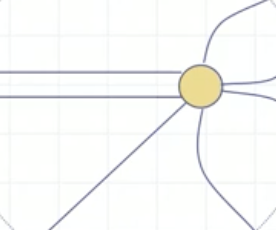
degree (차수) - undirected graph
Q. 만약 self-loop가 있다면, incident한 edge의 개수인지, 노드에 붙어있는 선의 개수인가?
A. 선의 개수이다
따라서, undirected graph의 self loop의 경우, incident한 edge의 개수에 2배를 해줘야함
in-degree : 들어오는 edge
out-degree : 나가는 edge
Handshaking Theorem
degree의 합은 edge 개수와 상관이 있다는 이론
Theorem
in an undirected graph : \(|E| = \frac{1}{2}\sum_{v\in V}^{}deg(v)\) edge의 개수는 차수의 합의 절반
in a directed graph : \(|E| = \sum_{v\in V}^{}deg^+(v)=\sum_{v\in V}^{}deg^-(v)\) in degree, out degree의 값은 edge개수와 같음
Lemma
The number of vertices of ddd degree must be even in an undirected graph
undirected 그래프에서 차수가 홀수인 노드는 항상 짝수개 존재한다
pf) 귀류법 사용
2|E| = Sum of even node's + sum of odd node's
2|E|는 짝수이므로 짝수 + 홀수는 짝수가 될 수 없으므로 모순
∴Handshaking Theorem을 실패하면 불가능한 그래프, 하지만 성공하더라도 가능하다고 단언할 수 없음
Q.
4쌍의 부부가 존재하고, 일부 사람들이 악수를 한다 (Symmetric - 대칭성)
또한, 한 사람당 한번만 한다. (simple graph)
부부간에는 악수를 하지 않고, 각자 악수한 인원을 말했더니 모든 가능한 수가 다 나왔다.
겹치는 수는 무엇인가?
A.
가능한 모든 경우는 0,1,2,3,4,5,6이다. 부부간엔 악수를 하지 않으므로 7은 제외한다
만약 한명이 0이라고 가정하자.
6이 들어갈 자리를 찾는다면, 무조건 0과 부부일 것이다. 부부를 제외한 모든 사람과 악수해야하기 때문이다.
한 쌍의 부부가 0,6이 가능하므로, 이를 제외하고 세 쌍의 부부만 생각하고 이때 가능한 경우는 1,2,3,4,5이다
같은 방법으로 한명이 1이면, 나머지와 모두 악수해야하는 5는 1과 5는 부부이다
이를 또 제외하여 두쌍의 부부로 만들고, 이를 반복하게 되면, 2와 4 / 3과 3이 나온다는 것을 알 수 있다
따라서 겹치는 수는 3이다
Graph Patterns
Complete Graphs \(K_n\)
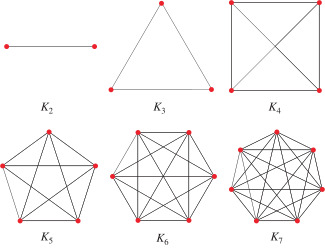
A simple graph is complete if every pair of distinct vertices share an edge
모든 edge로 모든 노드가 연결되어 있음
Cycle graph \(C_n\)

The cycle graph \(C_n\) is a circular graph with V = {0,1,2, ... n-1} where vertex i is connected to i+1 mon n and to i-1 mod n
n개짜리 노드가 존재하고, 노드가 바로 옆 노드와 edge로 연결되어 있음
* \(C_1\) & \(C_2\)의 경우 pseudo 그래프이므로 \(C_3\)부터 cycle graph로 취급함
Wheels \(W_n\)
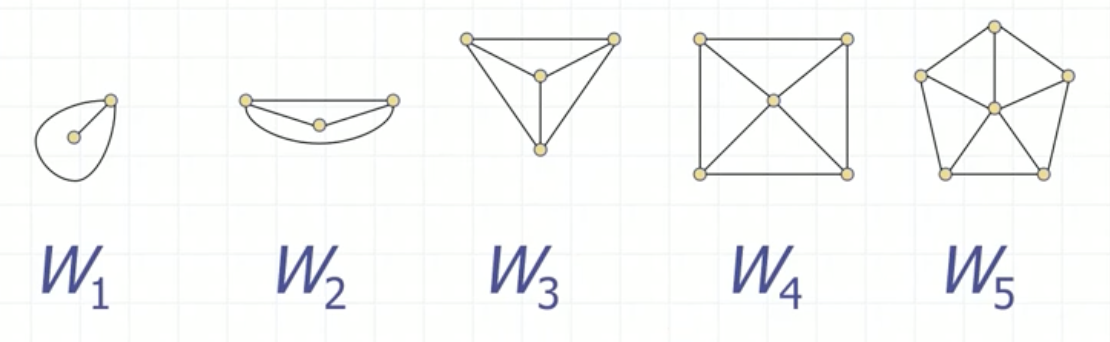
\(W_1\)은 pseudo 그래프, \(W_2\)는 multi graph이므로 wheel이라고 생각하지 않는다
The wheel graph \(W_n\) is just a cycle graph with an extra vertex in the middle
wheel 그래프는 cycle 그래프에서 중간에 노드 하나가 더 추가된 모양이다
Cube \(Q_n\)
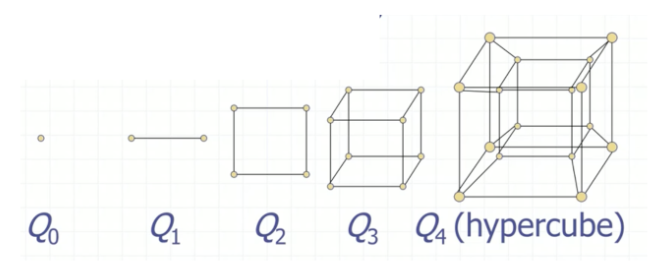
the n-cube \(Q_n\) is defined recursively \(Q_0\) is just a vertex. \(Q_{n+1}\) is gotten by taing 2 copies of \(Q_n\) and joining each vertex c of \(Q_n\) with its copy v
다음 차원을 만드는 방법 : 차원을 복사한 다음, 원본과 복사본을 edge로 이어줌
ex) \(Q_1\)을 복사한 후 원본과 복사본을 edge로 이으면 사각형 모양을 이룸
이와 같은 방법으로 우리가 알지 못하는 4차원의 모습을 만들 수 있음
노드에 주소 붙이기
\(Q_1\)의 경우 0, 1
\(Q_2\)의 경우 0,1을 그대로 복사한 후, 원본에는 앞에 0을 붙이고 복사본에는 1을 붙여 00 01 10 11을 만든다
이와 같은 방법으로, \(Q_n\)은 주소가 총 n자리이다
Bipartite Graphs
A simple graph is bipartite if V can be partitioned into \(V = V_1\bigcup V2\) so that any two adjacent vertices are in different parts of the parttition
V는 두 파트로 나누어질 수 있다. 이 파트, \(V_1\)과 \(V_2\)는 겹치는게 없고 합쳤을 때 전체가 되어야한다. 모든 인접한 노드가 다른 집합에 있어야하며, 모든 edge가 서로와 연결된다. (안에서 연결될 수 없음)
* \(V_1\) \(V_2\)로 나눌 수 있는 방법이 있는 것이지, 나눠서 제공되는 것이 아님 - 그래프의 특징임
bichromatic : vertices can be colored using two colors so that no two vertices of the same color are adjacent
edge가 존재하면, 다른 색으로 칠해서 다른 색이 분리가 되면 bipartite하다
Q. for which n is \(C_n\) bipartite
A. \(C_n\) is bipartiten is even.
n이 짝수면, 노드에 번호가 있다고 가정하면
홀수번 노드와 짝수번 노드는 다른 색을 가지게 된다
만약, n이 홀수이면 노드 n-1번과 0번이 같은 색을 가지게 되므로 모순이 생긴다
Planner Graph
edge가 교차하지 않도록 평면에 그릴 수 있는 그래프
즉, 이것도 그래프의 성질로 만약, 한가지 방법이라도 planner graph로 그릴 수 있다면, 그 그래프는 planner graph인 것이다.
Kuratowski's and Wagner's theorems
\(K_{3,3}\)과 \(K_5\)를 포함하는 그래프는 planner graph가 아니다
Complete Bipartite \(K_{m,n}\)
all possible edges exist in a simple bipartite graph with m red vertices and n green vertices
m개의 빨간 노드, n개의 초록 노드가 있을 때 이 두가지 색깔의 노드가 가능한 모든 edge가 연결되어있음
Bipartite Graph check
전진을 한 edge만 고르면 트리가 나오게 된다 - BFS/DFS에 상관 없이
노드에가 bipartite였고, 만약 같은 집합에 있는 노드의 색을 검은색 / 빨간색으로 칠했다면 red-black 트리의 형태가 나오게 된다
'CS > Data Structure' 카테고리의 다른 글
| HALTING Problem (0) | 2024.09.03 |
|---|---|
| Graph (Subgraphs, Unions, Isomorphism, Path) (0) | 2024.06.20 |
| Union Find (10) | 2024.06.13 |
| Tree Traversal & Parsing (0) | 2024.06.13 |
| Priority Queue (1) | 2024.06.12 |