대칭 암호화 방식
암호화와 복호화에 동일한 키가 사용되는 방식

암호학적 강도 (안전성)
- 혼돈 (confusion)과 확산(Diffusion)의 정도로 측정
- 혼돈 : 암호문의 통계적 성질과 평문의 통계적 성질의 관계를 난해하게 만드는 성질 / 암호문에서 평문의 특성을 알아내기 힘든 성질
-> 빈도 분석 등을 이용해서 복호화 할 수 없음 - 확산 : 각각의 평문 비트와 키 비트가 암호문의 모든 비트에 영향을 주는 성질 / 평문의 작은 변화가 암호문의 큰 변화로 이어지는 성질
-> 암호문과 원문을 연결짓기 힘듦
블록 암호
- 평문과 암호문이 고정된 크기의 블록으로 구성
각 블록을 독립적으로 따로 암호화 하면, 평문이 같은 블럭은 같은 암호를 생성한다. - 암호문은 평문의 반복되는 회전함수로 생산
- 회전 함수 입력은 전번 회전 출력과 키로 구성
- 종류 : EBC, CBC, CFB, OFB
CBC

2번째 블록에 암호문은 단순히 두번째 블록의 암호문만 생성하는 것이 아니라, 첫번째 블록의 암호문과 2번째 블록의 평문으로 암호화를 진행한다.
-> 따라서 같은 평문의 블록이 있어도 다른 암호문으로 나오게 된다
첫번째 블록은 이전 암호문이 없기 때문에
IV (초기 벡터)를 사용한다 : 고정된 값이나 랜덤 값을 사용한다
Q) 랜덤 값을 사용하는 경우에 어떻게 복호화 하는가?
A) 원래의 평문 앞에 IV를 붙여서 암호화를 수행한다. IV를 그대로 DES해서 넣는다.
복호화를 할 때는 반대로 DES를 하게 됨. 마지막에 되면 plain과 cipher을 xor한 값을 알게 된다.
xor의 특징 중 하나는 다른 하나를 xor하면 없어지게 됨
복호화를 할 때는 plain xor cipher xor cipher하면 plain만 남게 된다. (cipher은 이미 암호문에 나와있음)
페이스텔 암호
- 블록 암호 설계의 한 형태
- 평문을 좌우 반쪽으로 나눔 : 평문 \((L_0, R_0)\)
- 각 회전 i = 1,2,3, ... n에서 다음을 계산
- \(L_i = R_{i-1}\)
- \(R_i = L_{i-1} \oplus F(R_{i-1},K_i)\) : 왼쪽이 오른쪽으로 오면서 어떤 함수를 수행한다
- 여기서 F : 회전 함수, \(K_i\) : 보조키
- 암호문 : \((L_n, R_n)\)
DES
현재 사용되는 것은 AES와 3DES
- 16개의 회전 (또는 라운드)를 갖는 페이스텔 암호 -> 한번 라운드를 거칠 때마다 64비트 블록을 크로스 함
- 64비트의 블록 암호화 알고리즘 -> 평문을 64bit 블록 단위로 쪼개, 각 블록에 대해 암호문을 만듦
- 56비트 크기의 암호화 키 사용
- 생성 가능한 암호화 키는 최대 \(2^56\)가지
- 각 라운드는 48비트의 보조키를 사용
- 보조키는 56비트 키 중 48비트를 사용해 구성함
DES 암호화와 복호화 과정 (1round)
- S-Box를 이용한 혼돈과 확산
- 6비트를 4비트로 매핑
- 서로 다른 8개의 S-Box 사용
- 페이스텔 암호의 특징이였던 회전 함수 (F)의 역할을 S-Box, P-Box가 수행함 (이미 공개되어있음)
- S-Box : 어떤 입력 값이 주어졌을 때 어떻게 대체할지에 대한 것
- P-Box : 위치를 바꾸는 것
- 총 8개의 S-box 사용
- 총 16회 반복

복호화 시에는 같은 암호화 키, 같은 Sbox로 복호화할 수 있음

- 각 라운드의 input을 반으로 쪼개면 L,R이 된다.
- R은 그대로 L로 내린다.
- R을 비트 확장 시켜 32비트에서 48비트로 만든다.
- 각 라운드에서 사용될 key 값 (48bit)로 xor을 한다.
- S-boxes로 값을 대체하는 과정을 거침 (8개가 존재함) -> 32bit가 됨
- P-box로 위치를 바꿈
- L과 xor하여 결과 R을 생성한다
각 라운드의 키 만드는 법
- key를 28비트씩 나눈다
- 28비트씩 나눈 키를 shift과정을 통해 비트 위치를 바꾼
- 다시 합친 후 compress (DES 알고리즘에 정해져있음)
- 그냥 합친 것은 다음 key로 보냄
S-Box

48비트가 되면, 6bits 가 8개의 블록이 되게 되고, 이가 각각 s-box에 순차적으로 대응하여 substitution을 하게 된다.
32 bit -> 48bit

8개 블록의 4비트가 존재하는 것을 8개 블록의 6비트로 만드는 것이다
원래 4비트가 가지고 있는 값은 그대로 두고, 양 옆에 있는 bit를 가져와서 가져다가 붙인다.
맨 앞 뒤는 마지막과 맨 앞에서 가져온다
48bit -> 32bit
만약 6비트가 111000이라고 가정하자
행이 4개에 열이 16개인 표를 각 s-box가 가지고 있다.

가운데에 4자리와 맨 앞뒤 2자리를 구분한다.
4자리는 열, 2자리는 행이 된다
111000 -> 10 : 2, 1100 : 12이므로 3이라는 값으로 대체가 된다 -> 0011이 됨
P-box

위치가 바뀌게 되는 것
32비트가 서로 비트 값이 섞이게 된다.
지금 현재 그림의 표를 보면, 첫번째 비트에는 16번째 비트가 오고, 다음엔 7번째 비트 ... 이런 방식으로 섞이게 된다
이처럼 대칭키 알고리즘의 가장 큰 장점은
1. 구현이 쉽다
2. 실행 속도가 굉장히 빠르다
DES의 안전성
- 다수의 S-Box에 의존
- DC(Differenctial Cryptoanalysis), LC(Linear Cryptoanalysis), DES challenge등의 공격으로 분산 환경에서 병렬처리로 복호화 됨
- 전용 칩으로 56시간만에 복호화
- 분산 시스템으로 22시간만에 복호화
즉, 결국 \(2^56\)개의 키를 적용해보면 풀 수 있음
3DES (트리플 DES)
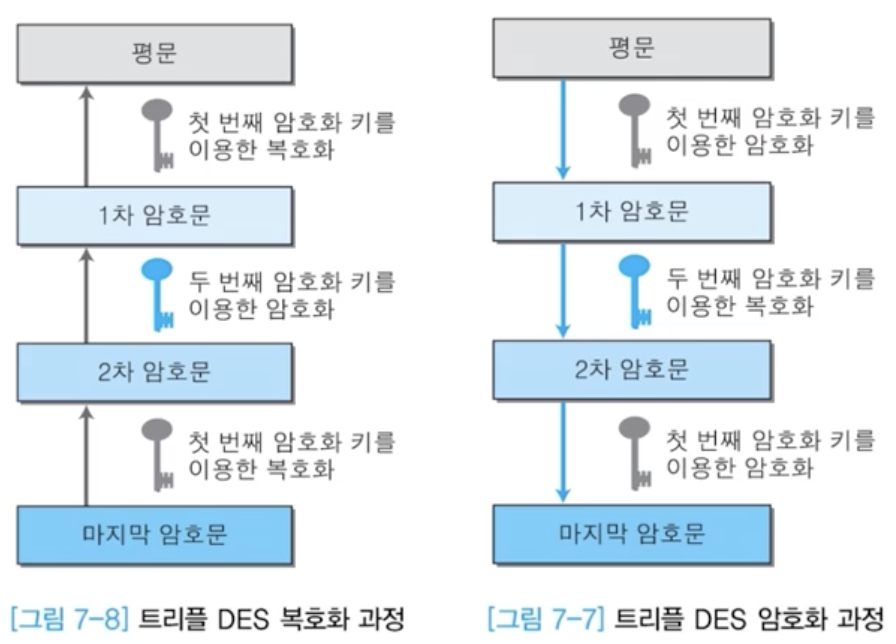
- DES의 복호화가 가능해짐에 따라 AES가 나오기 전까지 임시로 사용한 암호 알고리즘
- 2개의 암호화 키를 사용(112비트) -> 56비트 키 두번을 사용하는 것처럼 하여 112비트 키를 사용하는 것과 같은 효과를 내자
- C = E(D(E(P,K1),K2),K1)
- P = D(E(D(C,K1),K2),K1)
- DES에서 암호화 및 복호화 과정은 똑같다 (역순일 뿐)
- 암호화 과정의 가장 바깥 -> 복호화 과정의 가장 안
- 왜 2개의 키로 암호화 복호화 암호화 (EDE)하는가?
- 왜 2DES는 없는가?
2DES vs 3DES
2DES를 보자
C = D(E(P,K1), K2) -> 다른 키를 사용했기 때문에 복호화 되는 것은 아니다
두 개의 key를 사용하기 때문에 56bit + 56bit 하여 총 112bit의 key를 사용하는 것이다
즉, \(2^112\)개의 경우의 수가 생긴다.
따라서 \(2^112\)개를 수행해야한다.
그러면 3DES도 key를 두 개 사용하기 때문에 2DES에서 수행하는 것과 같지 않은가?
알려진 <P,C>가 주어진다
key가 무엇인지 알아내기 위해서는 \(2^112\)개의 key를 시도해봐야하는가?
C1 = E(P, K1)
C2 = D(C1, K2)
P에서 C1을 만들기 위해서는 \(2^56\)개의 키를 이용하여 총 n개의 암호문이 만들어지게 된다.
다시 K2에 대해서 복호화해서 평문을 알아내야하는데,
이를 반대로 암호문 C로부터 K2로 다시 C1을 만들기 위해서 \(2^56\)개를 시도할 수 있다.
이렇게 구해낸 두 개의 n개의 C1에서 같은 어떤 암호문이 존재한다.
따라서 이러한 MITM 기법을 이용하여 \(2^56 \times 2 = 2^57\)번의 수행만 있으면 된다
서로 다른 키를 2개를 이용했지만, 2개쓴 효과를 만들어내지 못한다.
따라서 3DES를 사용하면, 중간에 끼어들어도 \(2^112\)를 시도해야한다.
∴키를 여러개 쓴다고 안전성이 올라가는 것은 아니다
AES
리즈멘과 대먼의 Rijndeal 알고리즘 -> AES
128비트 암호화 블럭을 사용
키 size가 128에서 256까지이다
대칭키 암호 알고리즘의 장,단점
장점
- 연산이 매우 빠름
- 알고리즘이 쉽고 구현이 간단
단점
- 키 교환 (또는 분배)가 어려움 : 송신자와 수신자가 비밀리에 비밀키 공유
- 사용자가 늘어날수록 비밀키의 개수도 증가 : N명이 서로 비밀 통신을 하기 위해서는 (n)(n-1)/2개의 비밀키 필요
- 키를 비밀로 유지 : 키가 노출되면 모든 암호문이 복호됨
'Hacking > Cryptography' 카테고리의 다른 글
| [비대칭키 암호 시스템] RSA (0) | 2024.12.15 |
|---|---|
| [비대칭키 암호 시스템] Elgamal Encryption (1) | 2024.12.15 |
| [공개키 암호 시스템] 정수론 (0) | 2024.12.15 |
| 고전, 근대, 현대 암호 (2) | 2024.12.15 |
| [블록 암호] 운영모드 (1) | 2024.02.12 |