디피와 헬만 (Diffie-Hellman)
- 암호화 키 교환의 문제를 해결
- Diffie hellman Key Exchange Protocol -> 비대칭키의 개념 소개
- 이를 통해 다양한 암호 프로토콜이 생기게 됨
정수론 기초
Group
A group (S, \(\oplus\)) is a set S together with a binary operation \(\oplus\) defined on S for which the following properties hold
어떤 집합 S와 주어진 연산에 대해서 다음의 4가지 조건을 만족하면 group 이라고 한다
- Closure : \(\forall a,b\), we have \(a\oplus b \in S\) 연산에 대해서 닫혀있다
- Identity : \(\exists\) an \(e \in S\) s.t. \(e \oplus a = a \oplus e = a\), \(\forall a \in S\) 항등원이 존재한다
항등원과 나의 연산에 대해 결과가 그대로 나 인것 - Associatibity : \(\forall a, b, c \in S, (a \oplus b)\oplus c = a \oplus(b \oplus c)\). 결합 법칙 성립
- Inverse : For each \(a \in S\), \(\exists\) unique element \(b \in S\) s.t. \(a \oplus b = b \oplus a = e\) 역원 존재
ex) \((\mathbb{Z}, +)\) -> group
정수의 덧셈은 정수이다
정수 집합에 속하는 원소의 항등원 : 0
결합 법칙 성립함
덧셈에 대한 역원, -a가 존재한다
Abelian Group
If a group (S, \(\oplus\)) satisfies the commutative law \(a \oplus b = b \oplus a\), \(\forall a, b \in S\), then it is an abelian group
group들 중에 교환 법칙이 성립하면 abelian group이라고 한다
Finite Group
|S| = n for some integer n
어떤 집합이 group인데 원소의 개수가 유한개
Finite Group 생성 방법
The equivalence class(동치류) modulo n containing an integer a is
\([a]_n = \{a + kn | k \in Z\}\)
n으로 나눈 나머지가 a인 모든 집합
\(a \in [b]_n \Leftrightarrow a \equiv b\)(mod n)
저 a 는 모두 congruent하다
\(Z_n = \{[a]_n | a \leq a \leq n-1\}\)
\(Z_n = \{0, 1, ... n-1\}\)
따라서 Z 자체는 무한 집합이지만, 이를 n으로 나눈 나머지 값들의 집합은 n개를 가지는 유한 집합이 된다.
\(Z^*_n = \{[a]_n \in Z_n | gcd(a,n) = 1\}\)
n에 대해서 서로소인 나머지 값들을 \(Z^*_n\)이라 한다.
ex) \(Z_6 = \{0,1,2,3,4,5\}\)이고,, \(Z^*_6 = \{1,5\}\)
Addition \(+_n\) and multiplication \(\cdot_n\) modulo n for \(Z_n\)
If \(a \equiv a'\) (mod n) and \(b \equiv b'\) (mod n), then
\(a + b \equiv a' + b'\) (mod n),
\(ab \equiv a'b'\)(mod n)
=> \([a]_n +_n [b]_n = [a+b]_n\),
\([a]_n \cdot_n [b]_n = [ab]_n\)
각각 계산하는 것과, 따로 계산하는 것 모두 같은 결과이다
Finite abelian group
- 닫혀있음
- 항등원
- 결합법칙
- 역원
- 교환법칙
- 유한함
\(Z_n = \{0,1, ... n-1\}\) 이므로 일단 유한하다
additive group modulo n : \((Z_n, +_n)\)
1. 닫혀있음
a+b(mod n)은 무조건 0~n-1을 만들기 때문에 닫혀있다
2. 항등원
\(a \in Z_n\)에 대하여 a + x = a mod n 이 되는가? 에 대한 문제이다
x = 0이 되므로 항등원이 존재한다
3. 결합법칙
(a + b) + c mod n = a + (b+c) mod n은 같다.
각각을 mod n 하는 것과 동시에 하는 것이 같다는 것을 보임
4. 역원
- 가 존재하지 않는다
a + x mod 7 = 0
a + x = 7의 배수이면 된다.
즉, n의 배수가 되는 수가 있기만 하면 된다 -> kn
5. 교환법칙
a + b, b+ a 교환법칙이 성립한다.
multiplicative group modulo n : \((Z^*_n, \cdot_n)\), where \(Z^*_n = \{[a]_n \in Z_n | gcd(a,n) = 1\}\)
* \(Z_n\)에 대해서는 되지 않는 이유에 대해서 먼저 보이겠다.
-> 역원이 존재하지 않음
\(a \cdot x\) mod n = 1 mod n
문제는 \(Z_n\)에는 0이 있다. 0에서 무엇을 곱해도 0이기 때문에, 역원이 존재하지 않는다.
즉 애초에 \((Z_n, \cdot)\)은 group이 아니다.
나머지 조건들은 모두 성립한다.
1. 닫혀있음
\(a \cdot b\) mod n \(\in Z^*_n\)이다.
서로소는 곱해도 서로소가 된다.
2. 항등원
\(a \cot x\) mod n
x = 1이면 된다
3. 결합 법칙
아까 위에 각각 계산하는 것과 따로 계산하는 것 모두 상관 없다고 보임
4. 교환 법칙 : 성립한다
5. 역원
0을 포함하지 않기 때문에 가능하다
The (multiplicative) inverse of a : \(a^{-1} mod\ n\)
즉, \(a \cdot a^{-1} mod/ n \equiv 1 mod/ n\)
역원을 정의할 수 있으면, 나누기에 대한 정의도 할 수 있다.
Division in \(Z^*_n\) is defined by \(a / b \equiv ab^{-1} (mod/ n)\)
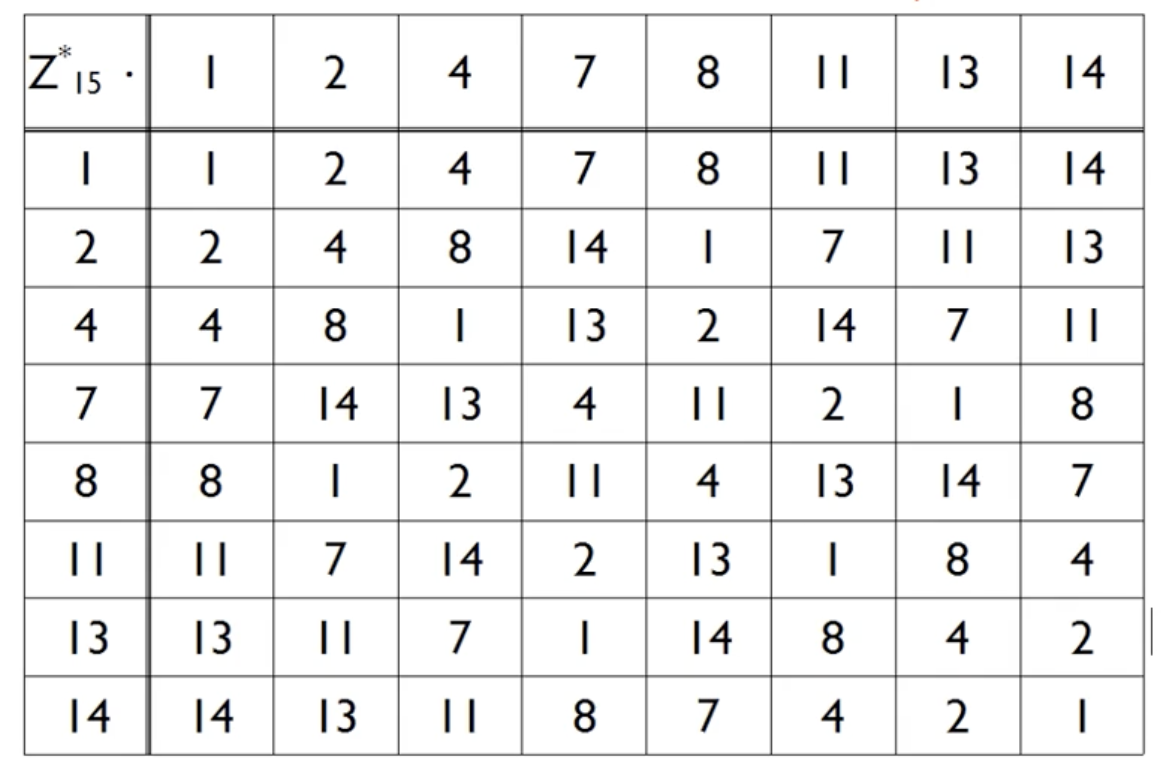
곱셈 결과를 나타내는 테이블이다
즉, 곱했을 때 1이 되는 것이 자기 자신의 역원이 되는 것이다
결과적으로 모두 역원이 존재한다.
Euler's phi function
\(|Z^*_n| = \varphi(n)\)
\(\varphi(n) = n\prod_{p|n}(1-\frac{1}{p})\), where p runs over all the primes dividing n
n에 대해서 n보다 작거나 같은 소수 중 n의 약수가 되는 소수들의 (1-1/p)를 곱해주면 된다
ex) \(Z^*_5 = \{1,2,3,4\}\) => \(\varphi(5) = 5 \times (1-\frac{1}{5}\) = 4\)
If, p is prime, then \(Z^*_p = \{1,2,... p-1\}\), and \(\varphi(p) = p-1\)
결국 p에 대해서 전부 서로소이므로 p-1이다
따라서 \(Z^*_p\)는 finite abelian group이 된다
Subgroups
If (S, \(\oplus\)) is a group, S' \(\subseteq\) S and (S', \(\oplus\)) is also a gorup, then (S', \(\oplus\)) is said to be a subgroup of (S, \(\oplus\)).
어떤 집합 s가 주어진 연산에 의해 group이면서, 이 부분집합도 group이라면 그것을 subgroup이라고 정의한다
Subgroups generated by an element
subgroup들을 어떻게 생성하는가?
- Define \(a^{(k)}\) for k ≥ 1 by \(a^{(k)} = a \oplus a \oplus a ... \oplus a\) (ktimes)
어떤 원소에 대해서 그 집합에 정의된 연산을 반복적으로 수행해서 얻은 값으로 생성할 수 있다. - \(S' = \{a, a\oplus a, a\oplus a\oplus a, .. \}\)
- For example, in the group \(Z_n\), \(a^{(k)} = ka\ mod\ n\)
- in the group \(Z^*_n\) , \(a^{(k)} = a^k\ mod\ n\)
<a> : the subgroup generated by a
<a> = \(\{a^{(k)} | k \leq 1\}\), a is a generator of <a>
ord(a) : the order of a (in the group S) : the least t > 0 s.t. \(a^{(t)} = e\) (항등원)
즉, \(a^{(k)}\)부터 반복되는 것이다. -> 즉, ord(a)는 서로 다른 값들의 개수 -> 결국 원소의 개수는 t개
Theorem
For any finite group (S, \(\oplus\)) and any \(a \in S\), the order of an element is equal to the size of the subgroup it generates, ord(a) = |<a>|.
And the sequence \(a^{(1)}, a^{(2)}, ...\) is periodic with period t = ord(a)
어떤 연산이 주어진 집합이 group이면, 그 원소 a로 subgroup을 생성할 수 있다.
이 subgroup은 주어진 연산을 반복하여 생성한다.
그 subgroup의 차수는, 그 subgroup의 원소의 개수와 같아진다
Powers of an Elements \((Z^*_n, \cdot)\)
consider the sequence of powers of a, modulo n where \(a \in Z^*_n\) : \(a^1, a^2,\), ... modulo n

\(Z^*_7\) = \{1,2,3,4,5,6\}\)
\(3 \in Z^*_7\)
3 mod 7, 9 mod 7, 27 mod 7의 의미와 같은 집합이 만들어진다.
따라서 표처럼 결과가 나오게 된다.
곱셈에 대한 항등원은 1이기 때문에 ord(3) = 6, |<3>| = 6이다
subgroup과 원래 group이 같다
Cyclic
- If \(ord_n(g)\) = \(|Z^*_n|\), then every element in \(Z^*_n\) is a power of g modulo n
만약, ord<g> = \(|Z^*_n|\) 인 경우 - g : a primitive root or generator of \(Z^*_n\)
- if \(Z^*_n\) contains a generator, the group \(Z^*_n\) is said to be cyclic
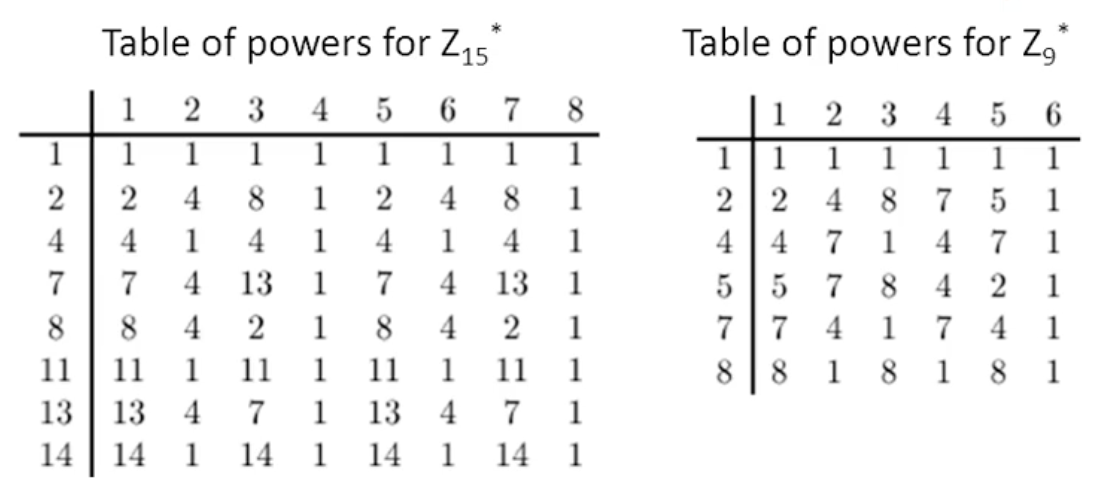
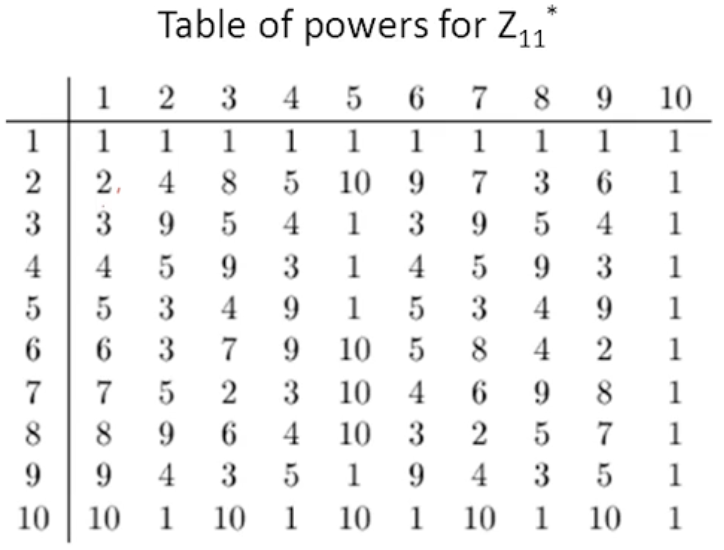
15는 cyclic 하지 않고, 9와 11은 cyclic 하다
9의 경우 ord(2), ord(5)가 생성자이다
지금 열은 \(|Z^*_n|\), \(\varphi(n)\)과 같다.
해당 원소의 갯수만큼 한 것은 결국 1이다.
[ Theorem ] Euler's Theorem
For any integer n > 1, \(a^{\varphi(n)} \equiv 1 (mod\ n)\) for all \(a \in Z^*_n\)
Fermat's Little Theorm
if P is prime, \(a^{p-1} \equiv 1 (mod\ p)\) for all \(a \in Z^*_p\)
Discrete Logarithm Problem
If g is a generator of \(Z^*_n\) and a is any element of \(Z^*_n\), then there exists a z s.t. \(g^z \equiv a (mod\ n)\),
This z is called the discrete logarithm of a, modulo n to the base g
임의의 g는 finite cyclic abeilan group이고, 이 생성자 g는 z승 했을 때 a가 되는 것을 discrete logarithm of a 이다.
[Theorem] Discrete Logarithm Theorem
If g is a generator of \(Z^*_n\), then the equation \(g^x \equiv g^y\)(mod n) holds iif the equation \(x \equiv y\)(mod \(\varphi(n)\)) holds
Discrete Logarithm Problem (DLP)
When g, \(z^*_n\) and y are given, DLP is to find x such that \(y \equiv g^x\) mod n
이러한 x를 찾는 것이 매우 어렵고 아직 solution이 존재하지 않는다
Primality Test
소수인 것을 어떻게 알 수 있는가?
가장 직관적이고 단순한 방법은 1부터 n-1까지 나누어지는지 확인하는 것
엄청나게 큰 숫자가 주어졌을 때 prime인지 아닌지 판단하는 법은 오일러 공식과 페르마 소정리를 활용하는 것이다
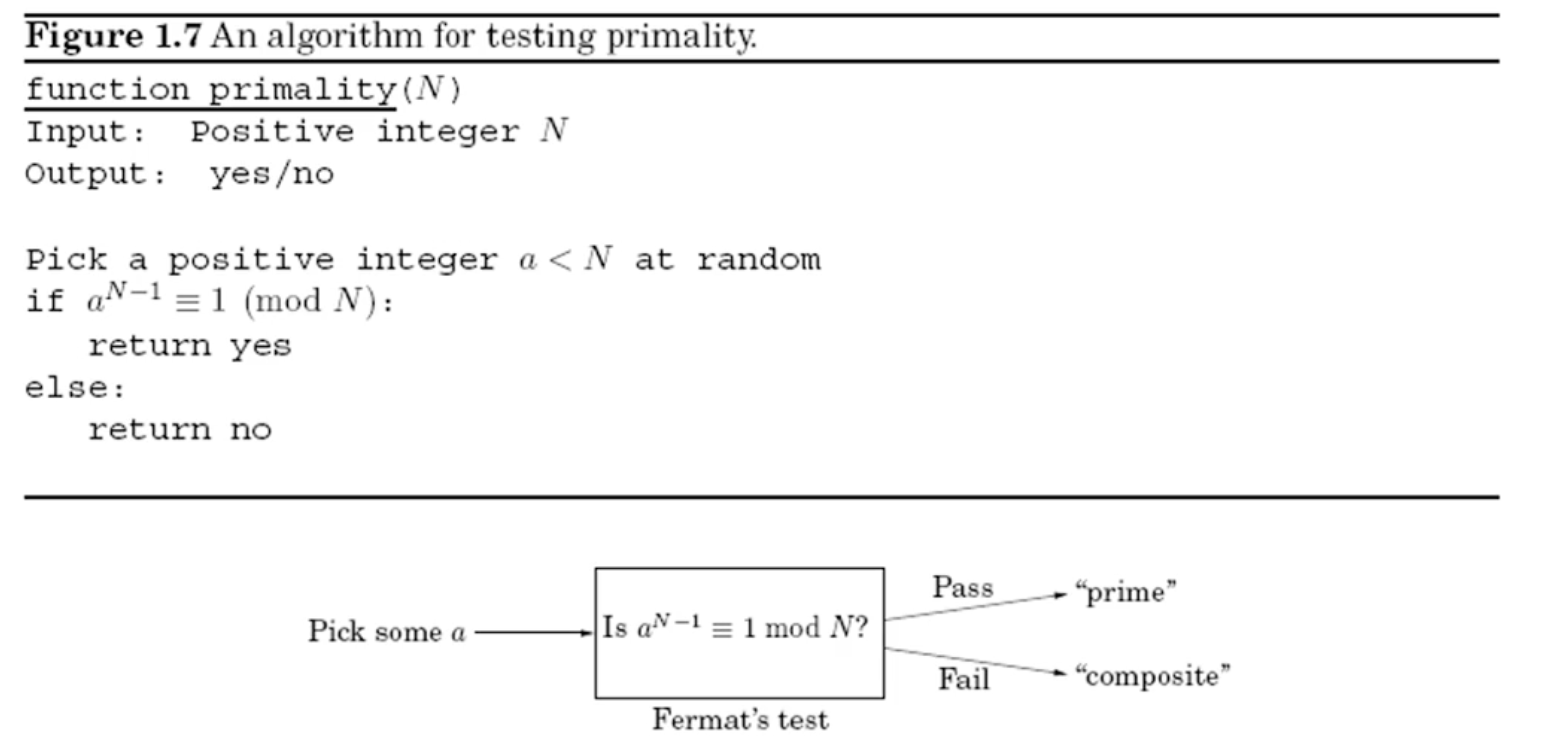
N이 소수이면 페르마 소정리를 만족할 것이다
문제는 prime이 아닌 것 (합성수)인데도 앞의 테스트를 통과하는 경우가 있다.
이러한 수들을 Carmichael numbers 라고 한다.
따라서 앞의 방법만으로도는 primality test를 할 수 없다.

여러개의 a에 대해서 확인할 수 있다.
prime이면 모두 다 통과하게 된다.
pr(when N is not prime) ≤ \(\frac{1}{2^k}\)가 되기 때문에 prime인지 아닌지 확인할 수 있다.
'Hacking > Cryptography' 카테고리의 다른 글
| [비대칭키 암호 시스템] RSA (0) | 2024.12.15 |
|---|---|
| [비대칭키 암호 시스템] Elgamal Encryption (1) | 2024.12.15 |
| [대칭키 암호 시스템] DES (0) | 2024.12.15 |
| 고전, 근대, 현대 암호 (2) | 2024.12.15 |
| [블록 암호] 운영모드 (0) | 2024.02.12 |