[블록 암호] 운영모드

다양한 크기의 데이터를 처리할 수 있도록 고안된 블록 암호의 사용 방법

Padding (패딩)

평문에 데이터를 붙여서 평문의 크기가 블록 크기의 배수가 되도록 만드는 과정

 

Bit Padding (비트 패딩)

마지막 블록에서 평문이 채우지 못하는 비트 중 최상위 비트를 1로 설정하고 나머지는 모두 0으로 채우는 패딩 기법

수신자 : 평문의 마지막 비트부터 처음으로 값이 1인 비트가 나올때까지를 패딩으로 인식할 수 있음 > 제거하여 평문 복구

 

* 평문의 크기가블록 크기의 배수인 경우 : 수신자의 메세지 일부를 패딩으로 오인하게 되는 문제 발생

→ 패딩으로 한 블록을 추가함

 

ex) 0101 1010 1000 0000

Byte Padding (바이트 패딩) : ANSI X.923

블록의 남는 바이트를 일반적으로 0으로 채우고, 마지막 바이트에 패딩의 길이를 기록

 

* 평문의 크기가 블록 크기의 배수인 경우 → 패딩으로 한 블록을 추가함

 

ex) 14 23 40 00 00 00 00 04

Byte Padding (바이트 패딩) : PKCS#7

추가할 패딩의 마이트 크기로 마지막 블록을 채우는 패딩 기법

 

* 평문의 크기가 블록 크기의 배수인 경우 → 패딩으로 한 블록을 추가함

 

ex) 12 39 00 29 04 04 04 04

---

운영모드

ECB (Electronic Code Book) 모드

블록들은 모두 같은 키로 암호화

• 각 블록이 독립적으로 암호화 됨
• 여러 블록을 병렬적으로 암호화 할 수 있음
• 암호학적 안전성이 부족

ECB (Dreamhack Cryptography> 블록암호 : 운영모드)

■ 취약점

▶약한 혼돈 성질 : 패턴이 암호화된 암호문에도 그대로 나타남

EBC 취약점 (Wikipedia Block cipher mode of operation )

ex) 한 픽셀을 한 블록으로 EBC하여 암호화 하면 원본 이미지의 패턴이 그대로 나타남

 

▶재전송 공격 : 어떤 데이터를 재전송하여 시스템이 의도치 않은 행동을 하게 한다 

→ 암호문과 행동을 알면 그 암호문의 일부가 무엇을 나타내는지 유추하여 재전송할 수 있음

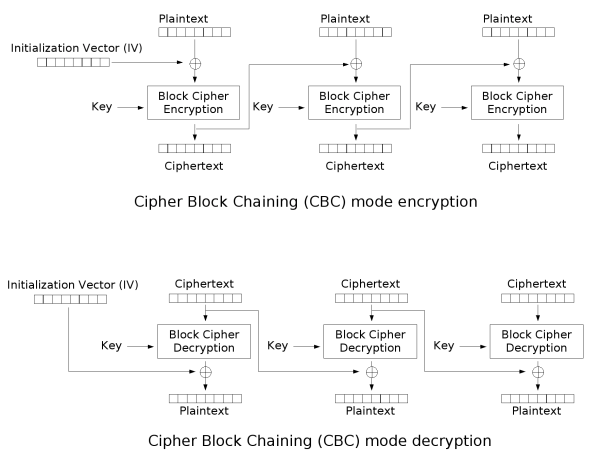
CBC (Cipher Block Chaining) 모드

암호화 하기 전에 블록을 직전 블록의 암호문과 XOR 
* 첫 번째 블록은 초기 벡터 (IV)라고 불리는 임의의 데이터와 XOR함

 

암호화 : \(C_0 = IV\), \(C_i = E_k(P_i \bigoplus C_{i-1})\), \(i \geq 1\)

복호화 : \(C_0 = IV\), \(P_i = D_k(C_i )\bigoplus C_{i-1}\), \(i \geq 1\)

초기 벡터 : Nonce(논스, number used only once) 라는 무작위 값을 사용 >  공격자가 알아도 안전성에 영향 없음

↔ 이를 조작한다면 복호화 결과의 첫번째 블록을 조작할 수 있음

• 초기 벡터의 무결성을 함께 보장해야함
• 여러 블록을 병렬적으로 암호화 할 수 없음
• 모든 암호문 블록을 알고 있으므로 병렬적으로 복호화 할 수 있음
• 재전송 공격에 강함
• 높은 혼돈성을 가짐

 

CBC (Dreamhack Cryptography> 블록암호 : 운영모드)

■ 취약점

▶ CBC Bit-Flipping Attack : 복호화 된 평문의 첫번째 블록을 조작하는 공격

첫 번째 암호문 블록의 복호화 과정 : \(P_1 = D_k(C_1)\bigoplus IV\)

초기 벡터 \(IV'\)로 조작하여 평문 블록을 \(P_1'\)으로 조작할 수 있음

$$ IV' = P_1 \bigoplus P_1' \bigoplus IV$$

 

CTR ( Counter ) 모드

nonce와 평문 블록의 인덱스 (counter)를 결합한 값을 입력
암호문 : 블록 암호의 출력과 평문 블록을 XOR하여 생성

* || 두 바이트 배열을 결합하는 기호

암호화 : \(C_i = P_i \bigoplus E_k (nonce || counter)\)

복호화 : \(P_i = C_i \bigoplus E_k (nonce || counter)\)

• 블록을 순서대로 암복호화 하지 않아도 됨
• 병렬로 암복호화 가능
• 구현이 간단함

CTR (Dreamhack Cryptography> 블록암호 : 운영모드)

reference

- Dreamhack Cryptography> 블록암호 : 운영모드